题目内容
14.双曲线$\frac{x^2}{3}-\frac{y^2}{6}=1$的渐近线方程是y=±$\sqrt{2}$x,离心率是$\sqrt{3}$.分析 根据题意,由双曲线的方程可得a、b,计算可得c的值,进而有双曲线的渐近线、离心率公式计算可得答案.
解答 解:根据题意,双曲线的方程为$\frac{x^2}{3}-\frac{y^2}{6}=1$,
其中a=$\sqrt{3}$,b=$\sqrt{6}$,则c=$\sqrt{6+3}$=3,
又由其焦点在x轴上,则其渐近线方程为:y=±$\sqrt{2}$x,
其离心率e=$\frac{c}{a}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$;
故答案为:y=±$\sqrt{2}$x,$\sqrt{3}$.
点评 本题考查双曲线的标准方程,关键要熟悉双曲线标准方程的形式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.S(A)表示集合A中所有元素的和,且A⊆{1,2,3,4,5},若S(A)能被3整除,则符合条件的非空集合A的个数是( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
9.公差不为零的等差数列{an}的前n项和为Sn.若a4是a3与a7的等比中项,S8=16,则S10等于( )
| A. | 18 | B. | 24 | C. | 30 | D. | 60 |
3.企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的8%缴纳,某企业员工甲在2010年至2016年各年中每月所缴纳的养老保险数额y(单位:元)与年份序号t的统计如表:
(1)求y关于t的线性回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$;
(2)按照这种变化趋势,利用(1)中回归方程,预测2017年该员工每月的平均工资(精确到0.1).
参考公式和数据:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$,$\sum_{i=1}^{7}$tiyi=13860,$\sum_{i=1}^{7}$ti2=140.
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 270 | 330 | 390 | 450 | 490 | 540 | 610 |
(2)按照这种变化趋势,利用(1)中回归方程,预测2017年该员工每月的平均工资(精确到0.1).
参考公式和数据:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$,$\sum_{i=1}^{7}$tiyi=13860,$\sum_{i=1}^{7}$ti2=140.
 从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.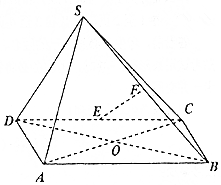 如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.
如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.