题目内容

如图示，在圆O中，若弦AB=6，AC=10，则
AO
•
BC
的值为（　　）
A、-16B、-2C、32D、16
考点：平面向量数量积的运算
专题：平面向量及应用
分析：先计算 
AO
•
AB
、
AO
•
AC
，再利用 
AO
•
BC
=
AO
•(
AC
-
AB
)，即可求得结论．
解答： 解：设圆的半径等于R，则
AO
•
AB
=R×6×cos∠OAB=R×6×
6
2R
=18，
AO
•
AC
=R×10×cos∠OAC=R×10×
10
2R
=50，
∴
AO
•
BC
=
AO
•(
AC
-
AB
)=
AO
•
AC
-
AO
•
AB
=50-18=32，
故选：C．
点评：本题主要考查向量在几何中的应用等基础知识，解答关键是利用向量数量积的几何意义，属于中档题．
练习册系列答案
相关题目
刘、李两家各带一个小孩一起到公园游玩，购票后排队依次入园．为安全起见，首尾一定要有两位爸爸，另外，两位小孩一定要排在一起，则这6人入园的顺序排法种数为
 
．
设正项等比数列{an}的前n项积为Tn，若T9=1，则a4•a6=
 
．
若复数z2+2=0，则z3等于（　　）
A、±2
2
B、2
C、±2
2
i
D、-2
2
i
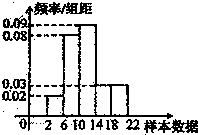若容量为100的某样本的频率分布直方图如图所示，则根据该频率分布直方图可以估计出样本数据落在[14，18）内的频数a的值为（　　）
A、8B、12C、32D、36
已知连续函数y=f（x），有f（a）f（b）＜0 ）（a＜b），则y=f（x）（　　）
A、在区间[a，b]上可能没有零点
B、在区间[a，b]上至少有一个零点
C、在区间[a，b]上零点个数为奇数个
D、在区间[a，b]上零点个数为偶数个
一个长、宽分别为4和2的长方形内接于圆（如图），质地均匀的一粒石子落入图中（不计边界），则落在长方形内的概率等于（　　）
A、
3
10π
B、
8
5π
C、
3
4π
D、20π
一位母亲纪录了儿子3到9岁的身高数据（略），她根据这些数据建立的身高y（cm）与年龄x的回归模型为
y
=7.19x+73.93，用此模型预测孩子10岁时的身高，则有（　　）
A、身高一定是145.83cm
B、身高在145.83cm左右
C、身高在145.83cm以上
D、身高在145.83cm以下
平面向量
a
，
b
中，若
a
=（4，-3），|
b
|=1，且
a
•
b
=5，则向量
b
=（　　）
A、（
4
5
，-
3
5
）
B、（-
4
5
，
3
5
）
C、（
4
5
，
3
5
）
D、（-
4
5
，
3
5
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网