题目内容
 一个长、宽分别为4和2的长方形内接于圆(如图),质地均匀的一粒石子落入图中(不计边界),则落在长方形内的概率等于( )
一个长、宽分别为4和2的长方形内接于圆(如图),质地均匀的一粒石子落入图中(不计边界),则落在长方形内的概率等于( )A、
| ||||
B、
| ||||
C、
| ||||
| D、20π |
考点:几何概型
专题:计算题,概率与统计
分析:确定矩形的面积、圆的面积,利用几何概率公式,可得结论.
解答:
解:由题意,矩形的面积S=4×2=8
圆的直径为
=2
,圆的面积S′=5π
记“质地均匀的一粒石子落入长方形内”为事件B,由几何概率的计算公式可得P(B)=
.
故选:B.
圆的直径为
| 16+4 |
| 5 |
记“质地均匀的一粒石子落入长方形内”为事件B,由几何概率的计算公式可得P(B)=
| 8 |
| 5π |
故选:B.
点评:本题主要考查了与面积有关的几何概率公式的应用,解题中的关键是要分别求出矩形及圆的面积,属于公式的简单应用.

练习册系列答案
相关题目
下列函数表示同一个函数是( )
A、y=x与y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=x与y=
|
如图示,在圆O中,若弦AB=6,AC=10,则
•
的值为( )

| AO |
| BC |

| A、-16 | B、-2 | C、32 | D、16 |
函数f(x)=
•
的定义域是( )
| 4-x |
| x+1 |
| A、[-1,+∞) |
| B、(-∞,-1] |
| C、[-1,4] |
| D、(-1,4) |
下列函数中,满足“对?x1,x2∈(0,+∞),当x1<x2,都有f(x1)>f(x2)”的是( )
| A、f(x)=x2 | ||
| B、f(x)=lnx | ||
| C、f(x)=-|x+2| | ||
D、f(x)=(
|
已知点A、B、C为椭圆
+y2=1上三点,其中A(1,
),且△ABC的内切圆圆心在直线x=1上,则△ABC三边斜率和为( )
| x2 |
| 4 |
| ||
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
圆x2+y2+4x-2y+4=0的点到直线y=x-1上的最近距离为( )
A、2
| ||
B、
| ||
C、2
| ||
| D、1 |
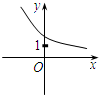 f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是
f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是