题目内容
设正项等比数列{an}的前n项积为Tn,若T9=1,则a4•a6= .
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:利用正项等比数列{an}的前n项积为Tn,T9=1,可得a1•q4=1,即可求a4•a6.
解答:
解:∵正项等比数列{an}的前n项积为Tn,T9=1,
∴a19•q1+2+…+8=1,
∴a1•q4=1,
∴a4•a6=(a1•q3)•a1•q5=(a1•q4)2=1,
故答案为:1.
∴a19•q1+2+…+8=1,
∴a1•q4=1,
∴a4•a6=(a1•q3)•a1•q5=(a1•q4)2=1,
故答案为:1.
点评:本题考查等比数列的性质,得出a1•q4=1是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=ax2+c(a≠0),若
f(x)dx=f(x0),则x0的值为( )
| ∫ | 1 0 |
A、±
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数表示同一个函数是( )
A、y=x与y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=x与y=
|
如图示,在圆O中,若弦AB=6,AC=10,则
•
的值为( )

| AO |
| BC |

| A、-16 | B、-2 | C、32 | D、16 |
圆x2+y2+4x-2y+4=0的点到直线y=x-1上的最近距离为( )
A、2
| ||
B、
| ||
C、2
| ||
| D、1 |
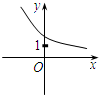 f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是
f(x)=ax+b的图象如图,其中a、b为常数,则下列结论正确的是