题目内容
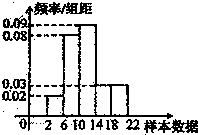 若容量为100的某样本的频率分布直方图如图所示,则根据该频率分布直方图可以估计出样本数据落在[14,18)内的频数a的值为( )
若容量为100的某样本的频率分布直方图如图所示,则根据该频率分布直方图可以估计出样本数据落在[14,18)内的频数a的值为( )| A、8 | B、12 | C、32 | D、36 |
考点:频率分布直方图
专题:概率与统计
分析:利用频率分布直方图先求出样本数据落在[14,18)内的频率,由此能求出频数a的值.
解答:
解:∵样本数据落在[14,18)内的频率为0.03×4=0.12,
∴样本数据落在[14,18)内的频数a=100×0.12=12.
故选:B.
∴样本数据落在[14,18)内的频数a=100×0.12=12.
故选:B.
点评:解决频率分布直方图的有关特征数问题,利用众数是最高矩形的底边中点;中位数是左右两边的矩形的面积相等的底边的值;平均数等于各个小矩形的面积乘以对应的矩形的底边中点的和.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
下列函数表示同一个函数是( )
A、y=x与y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=x与y=
|
已知函数f(x)=
,若f(a-1)+f(a)>0,则实数a的取值范围是( )
|
A、a>
| ||
| B、a>1 | ||
C、a<
| ||
| D、a<1 |
如图示,在圆O中,若弦AB=6,AC=10,则
•
的值为( )

| AO |
| BC |

| A、-16 | B、-2 | C、32 | D、16 |
函数f(x)=
•
的定义域是( )
| 4-x |
| x+1 |
| A、[-1,+∞) |
| B、(-∞,-1] |
| C、[-1,4] |
| D、(-1,4) |
已知点A、B、C为椭圆
+y2=1上三点,其中A(1,
),且△ABC的内切圆圆心在直线x=1上,则△ABC三边斜率和为( )
| x2 |
| 4 |
| ||
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
棱长为a的正方体内切一球,该球的表面积为( )
| A、πa2 |
| B、2πa2 |
| C、3πa2 |
| D、4πa2 |