题目内容
给出定义:若函数f(x)在(a,b)上可导,即f′(x)存在,且导函数f′(x)在(a,b)上也可导,则称f(x)在(a,b)上存在二阶导函数,记f″(x)=(f′(x))′.若f″(x)<0在(a,b)上恒成立,则称函数f(x)在(a,b)上为凸函数.已知函数f(x)=
x4-
mx3-
x2,若对任意实数m满足|m|≤2时,函数f(x)在(a,b)上为凸函数,则b-a的最大值是 .
| 1 |
| 12 |
| 1 |
| 6 |
| 3 |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:先求出f″(x),问题转化为当|m|≤2时,mx>x2-3恒成立,讨论当x=0时,x>0,x<0的情况,从而求出x的范围,进而解出答案.
解答:
解:∵f′(x)=
x3-
mx2-3x,
∴f″(x)=x2-mx-3,
当|m|≤2时,f″(x)=x2-mx-3<0恒成立,
?当|m|≤2时,mx>x2-3恒成立.
当x=0时,f″(x)=-3<0显然成立.
当x>0,x-
<m.
∵m的最小值是-2.
∴x-
<-2.
从而解得0<x<1,
当x<0,x-
>m,
∵m的最大值是2,∴x-
>2,
从而解得-1<x<0.
综上可得-1<x<1,从而(b-a)max=1-(-1)=2.
| 1 |
| 3 |
| 1 |
| 2 |
∴f″(x)=x2-mx-3,
当|m|≤2时,f″(x)=x2-mx-3<0恒成立,
?当|m|≤2时,mx>x2-3恒成立.
当x=0时,f″(x)=-3<0显然成立.
当x>0,x-
| 3 |
| x |
∵m的最小值是-2.
∴x-
| 3 |
| x |
从而解得0<x<1,
当x<0,x-
| 3 |
| x |
∵m的最大值是2,∴x-
| 3 |
| x |
从而解得-1<x<0.
综上可得-1<x<1,从而(b-a)max=1-(-1)=2.
点评:本题考查了导数的应用,不等式的解法,考查转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知{an}是等差数列,其前n项和为Sn,若a3=5-a2,则S4=( )
| A、9 | B、10 | C、11 | D、12 |
两个集合A与B之差记作“A/B”,定义A/B={x|x∈A,且x∉B|,如果集合A={x||x-2|≤1},B={x|log2x≥1,x∈R},那么A/B等于( )
| A、{x||x-2|≤1} |
| B、{x|x<2,或x≥2} |
| C、{x|1≤x<2} |
| D、{x|0<x≤1} |
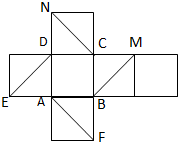 如图,为正方体的平面展开图,在这个正方体中
如图,为正方体的平面展开图,在这个正方体中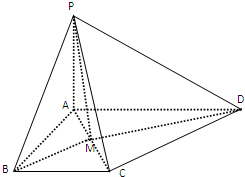 如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.
如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.