题目内容
从坐标原点O作曲线y=lnx的切线OP(P为切点),再过切点P引切线的垂线L,L与y轴的交点为Q.
(Ⅰ)求点P及点Q的坐标;
(Ⅱ)证明:点P是曲线y=lnx上距离点Q最近的点.
(Ⅰ)求点P及点Q的坐标;
(Ⅱ)证明:点P是曲线y=lnx上距离点Q最近的点.
考点:利用导数研究曲线上某点切线方程,两点间距离公式的应用
专题:导数的综合应用
分析:(Ⅰ)求出函数的导数,利用导数的几何意义以及直线垂直的位置关系即可求点P及点Q的坐标;
(Ⅱ)求出Q到直线OP的距离与|PQ|的关系即可得到结论.
(Ⅱ)求出Q到直线OP的距离与|PQ|的关系即可得到结论.
解答:
解:(Ⅰ)函数的f(x)的导数f′(x)=
,设切点为P(a,lna),
则切线斜率k=
,则切线方程为y-lna=
(x-a)=
x-1,
∵直线过原点,∴-lna=-1,
解得a=e,即P(e,1).即切线方程为y-1=
(x-e),
过切点P引切线的垂线L,则垂线L的斜率k=-e,
则对应方程为y-1=-e(x-e),
令x=0,则y=1+e2,
即Q的坐标为(0,1+e2);
(Ⅱ)由(Ⅰ)知过原点与y=lnx的切线方程为y=
x,
即x-ey=0,
则Q到直线x-ey=0的距离d=
=e•
,
而|QP|=
=
=e•
=d,
∴点Q到直线OP的距离为|QP|,
即点P是曲线y=lnx上距离点Q最近的点,
| 1 |
| x |
则切线斜率k=
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∵直线过原点,∴-lna=-1,
解得a=e,即P(e,1).即切线方程为y-1=
| 1 |
| e |

过切点P引切线的垂线L,则垂线L的斜率k=-e,
则对应方程为y-1=-e(x-e),
令x=0,则y=1+e2,
即Q的坐标为(0,1+e2);
(Ⅱ)由(Ⅰ)知过原点与y=lnx的切线方程为y=
| 1 |
| e |
即x-ey=0,
则Q到直线x-ey=0的距离d=
| |e(1+e2)| | ||
|
| 1+e2 |
而|QP|=
| e2+(1+e2-1)2 |
| e2+e4 |
| 1+e2 |
∴点Q到直线OP的距离为|QP|,
即点P是曲线y=lnx上距离点Q最近的点,
点评:本题主要考查导数的综合应用,利用导数求出切线斜率是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
设f(x)=
+2x,0<a<b<e,则( )
| lnx |
| x |
| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、f(a)f(b)>0 |
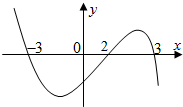 若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A、f(x)有极大值f(3)和极小值f(2) |
| B、f(x)有极大值f(-3)和极小值f(2) |
| C、f(x)有极大值f(3)和极小值f(-3) |
| D、f(x)有极大值f(-3)和极小值f(3) |
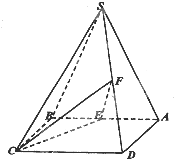 如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=
如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=