题目内容
1.若实数x,y满足不等式组$\left\{\begin{array}{l}x+2y≤2\\ x≥0\\ y≥0\end{array}\right.$,则当y≤ax+a-1恒成立时,实数a的取值范围是a≥2.分析 作出不等式组对应的平面区域,利用目标函数的几何意义结合数形结合进行求解即可.
解答 解:作出不等式组对应的平面区域如图:
直线y=ax+a-1=a(x+1)-1,过定点D(-1,-1),
y≤ax+a-1恒成立等价为可行域都在直线y=ax+a-1下方,
则由图象知只要A(0,1)满足y≤ax+a-1且a>0即可,
即$\left\{\begin{array}{l}{a>0}\\{1≤a-1}\end{array}\right.$得$\left\{\begin{array}{l}{a>0}\\{a≥2}\end{array}\right.$,即a≥2,
故答案为:a≥2
点评 本题主要考查线性规划的应用,根据可行域与直线的关系结合数形结合是解决本题的关键.

练习册系列答案
相关题目
11.已知正方形ABCD的边长为2,H是边DA的中点,在正方形ABCD内部随机取一点P,则满足|PH|<$\sqrt{2}$的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{8}+\frac{1}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{4}+\frac{1}{4}$ |
9.已知点A(-1,1),B(2,-2),若直线l:x+my+m=0与线段AB(含端点)相交,则实数m的取值范围是( )
| A. | (-∞,$\frac{1}{2}$]∪[2,+∞) | B. | [$\frac{1}{2}$,2] | C. | (-∞,-2]∪[-$\frac{1}{2}$,+∞) | D. | [-$\frac{1}{2}$,-2] |
16.设Sn为等差数列{an}的前n项的和a1=1,$\frac{{{S_{2017}}}}{2017}-\frac{{{S_{2015}}}}{2015}=1$,则数列$\left\{{\frac{1}{S_n}}\right\}$的前2017项和为( )
| A. | $\frac{2017}{1009}$ | B. | $\frac{2017}{2018}$ | C. | $\frac{1}{2017}$ | D. | $\frac{1}{2018}$ |
6.直线$\sqrt{3}x+y-a=0$的倾斜角为( )
| A. | 30° | B. | 150° | C. | 60° | D. | 120° |
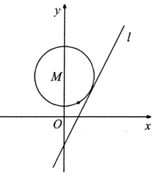 已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).
已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).