题目内容
函数f(k)=
(k>0)的最大值为 .
| 4k+1 |
| (2k+3)2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用,不等式的解法及应用
分析:利用换元法,结合基本不等式,即可得出结论.
解答:
解:设4k+1=t(t>1),则y=
=
=
,
∵t+
≥2
=10(当且仅当t=5,即k=1时取等号),
∴y≤
=
,
∴函数f(k)(k>0)的最大值为
,
故答案为:
.
| t | ||
[
|
| 4t |
| t2+10t+25 |
| 4 | ||
t+
|
∵t+
| 25 |
| t |
t•
|
∴y≤
| 4 |
| 10+10 |
| 1 |
| 5 |
∴函数f(k)(k>0)的最大值为
| 1 |
| 5 |
故答案为:
| 1 |
| 5 |
点评:本题考查基本不等式在求函数最值问题中的应用,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
老师在班级50名学生中,依次抽取班号为4,14,24,34,44的学生进行作业检查,老师运用的抽样方法是( )
| A、随机数法 | B、抽签法 |
| C、系统抽样 | D、以上都是 |
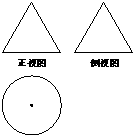 已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于
已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于