题目内容
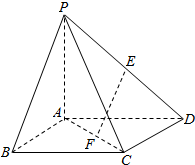 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且| DE |
| DP |
| AF |
| AC |
(Ⅰ)若λ=
| 1 |
| 2 |
(Ⅱ)求三棱锥E-FCD体积最大值.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)分别取PA和AB中点M、N,连接MN、ME、NF,四边形MEFN为平行四边形.由此能证明EF∥平面PAB.
(Ⅱ)在平面PAD内作EH⊥AD于H,则EH⊥平面ADC,EH∥PAEH=λPA=λ.S△DFC=(1-λ)S△ADC=
,由此能求出三棱锥E-FCD体积最大值.
(Ⅱ)在平面PAD内作EH⊥AD于H,则EH⊥平面ADC,EH∥PAEH=λPA=λ.S△DFC=(1-λ)S△ADC=
| 1-λ |
| 2 |
解答:
(Ⅰ)证明:分别取PA和AB中点M、N,
连接MN、ME、NF,则NF
AD,ME
AD,
所以NF
ME,∴四边形MEFN为平行四边形.
∴EF∥MN,又EF?平面PAB,MN?平面PAB,
∴EF∥平面PAB.
(Ⅱ)解:在平面PAD内作EH⊥AD于H,
因为侧棱PA⊥底面ABCD,
所以平面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,
所以EH⊥平面ADC,所以EH∥PA.
因为
=λ(0<λ<1),所以
=λ,EH=λPA=λ.
=
=1-λ,S△DFC=(1-λ)S△ADC=
,
VE-DFC=
×
×λ=
=
≤
,(0<λ<1),
∴三棱锥E-FCD体积最大值
.

连接MN、ME、NF,则NF
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
所以NF
| ∥ |
. |
∴EF∥MN,又EF?平面PAB,MN?平面PAB,
∴EF∥平面PAB.
(Ⅱ)解:在平面PAD内作EH⊥AD于H,
因为侧棱PA⊥底面ABCD,
所以平面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,
所以EH⊥平面ADC,所以EH∥PA.
因为
| DE |
| DP |
| EH |
| PA |
| S△DFC |
| S△ADC |
| CF |
| CA |
| 1-λ |
| 2 |
VE-DFC=
| 1 |
| 3 |
| 1-λ |
| 2 |
| λ-λ2 |
| 6 |
-(λ-
| ||||
| 6 |
| 1 |
| 24 |
∴三棱锥E-FCD体积最大值
| 1 |
| 24 |
点评:本题考查直线与平面平行的证明,考查三棱锥的体积的最大值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的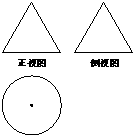 已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于
已知某几何体的三视图如图所示,其正视图与侧视图都是边长为2的等边三角形,则该几何体的体积等于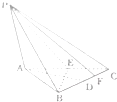 在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.
在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.