题目内容
三个半径均为3的球O1、O2、O3与半径为1的球l两两外切，则以O1、O2、O3和l为四个顶点的三棱锥外接球的半径为 ．
考点：球的体积和表面积
专题：空间位置关系与距离
分析：根据题意得出三棱锥底面边长为6，侧棱长为4的正三棱锥L=O1O2O3，利用正三角形O1O2O3的中心，求出LM=
=2，根据R2=（R-2）2+（2
）2求解即可．
| 16-12 |
| 3 |
解答：
解：∵三个半径均为3的球O1、O2、O3与半径为1的球l两两外切，以O1、O2、O3和l为四个顶点的三棱锥
∴三棱锥底面边长为6，侧棱长为4的正三棱锥L=O1O2O3，
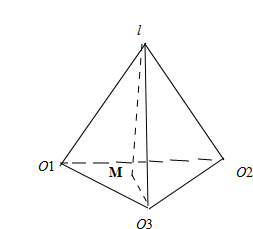
M为正三角形O1O2O3的中心，
MO3=2
，LM=
=2，
∴设三棱锥外接球的半径为R，
∴R2=（R-2）2+（2
）2，
解得：R=4，
故答案为：4．
∴三棱锥底面边长为6，侧棱长为4的正三棱锥L=O1O2O3，
M为正三角形O1O2O3的中心，
MO3=2
| 3 |
| 16-12 |
∴设三棱锥外接球的半径为R，
∴R2=（R-2）2+（2
| 3 |
解得：R=4，
故答案为：4．
点评：本题考查了空间几何体的性质，构造正三棱锥求解即可，属于中档题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
已知定义在（-1，1）上的函数f （x），其导函数为f′（x）=l+cosx，且f（0）=0，如果f（1-x）+f（l-x2）＜0，则实数x的取值范围为（ ）
| A、（0，1） | ||||
B、（1，
| ||||
C、(-2，-
| ||||
D、（1，
|
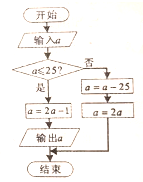某班有49位同学玩“数字接龙”游戏，具体规则按如图所示的程序框图执行（其中a为座位号），并以输出的值作为下一个输入的值，若第一次 输入的值为8，则第三次输出的值为（ ）| A、8 | B、15 | C、29 | D、36 |
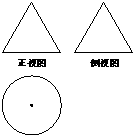已知某几何体的三视图如图所示，其正视图与侧视图都是边长为2的等边三角形，则该几何体的体积等于函数f（x）=
的值域为 （ ）
| 2x-1 |
| A、[-1，+∞） |
| B、（-∞，-1] |
| C、（-1，-∞） |
| D、[0，+∞） |