题目内容
给出四个区间：①（0，1）；②（1，2）；③（2，3）；④（3，4），则函数f（x）=2x+x-4的零点所在的区间是这四个区间中的哪一个： （只填序号）
考点：函数零点的判定定理
专题：计算题,函数的性质及应用
分析：易知函数f（x）=2x+x-4是定义域上的增函数，代入端点求函数值即可．
解答：
解：函数f（x）=2x+x-4是定义域上的增函数，
f（0）=1+0-4＜0；
f（1）=2+1-4＜0；
f（2）=4+2-4＞0；
故函数f（x）=2x+x-4的零点所在的区间是（1，2）；
故答案为：②．
f（0）=1+0-4＜0；
f（1）=2+1-4＜0；
f（2）=4+2-4＞0；
故函数f（x）=2x+x-4的零点所在的区间是（1，2）；
故答案为：②．
点评：本题考查了函数零点判定定理的应用，属于基础题．
练习册系列答案
相关题目
已知函数y=Asin（ωx+φ）（A＞0，|φ|＜π）的一段图象如图所示．已知定义在（-1，1）上的函数f （x），其导函数为f′（x）=l+cosx，且f（0）=0，如果f（1-x）+f（l-x2）＜0，则实数x的取值范围为（ ）
| A、（0，1） | ||||
B、（1，
| ||||
C、(-2，-
| ||||
D、（1，
|
一个透明的球形装饰品内放置了两个公共底面的圆锥，且这两个圆锥的顶点和底面圆周都在这个球面上，如图，已知圆锥底面面积是这个球面面积的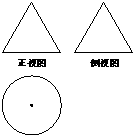
已知某几何体的三视图如图所示，其正视图与侧视图都是边长为2的等边三角形，则该几何体的体积等于