题目内容
2. 已知函数f(x)=$\frac{1}{2}$sinωx+$\frac{\sqrt{3}}{2}$cosωx(ω>0)的周期为π.
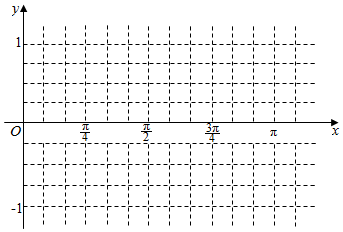
已知函数f(x)=$\frac{1}{2}$sinωx+$\frac{\sqrt{3}}{2}$cosωx(ω>0)的周期为π.(Ⅰ)求ω的值,并在下面提供的坐标系中画出函数y=f(x)在区间[0,π]上的图象;
(Ⅱ)函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换得到.
分析 (Ⅰ)由条件利用三角恒等变换化简函数的解析式为f(x)=sin(ωx+$\frac{π}{3}$),由此根据周期为π求得ω的值.根据五点法,求出对应的五点,即可画出函数y=f(x)在区间[0,π]上的图象.
(Ⅱ)由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:(Ⅰ)∵f(x)=$\frac{1}{2}$sinωx+$\frac{\sqrt{3}}{2}$cosωx=sin(ωx+$\frac{π}{3}$),
∴T=$\frac{2π}{ω}$=π,解得:ω=2,
∴f(x)=sin(2x+$\frac{π}{3}$),
列表:
| x | -$\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| 2x+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sin(2x+$\frac{π}{3}$) | 0 | 1 | 0 | -1 | 0 |

(Ⅱ)把y=sinx的图象向左平移$\frac{π}{3}$个单位,可得y=sin(x+$\frac{π}{3}$)的图象;
再把所得图象上的点的横坐标变为原来的$\frac{1}{2}$倍,可得y=sin(2x+$\frac{π}{3}$)的图象.
点评 本题主要考查三角恒等变换,正弦函数的周期性,函数y=Asin(ωx+φ)的图象变换规律,考查了五点法作函数y=Asin(ωx+φ)的图象,属于基础题.

练习册系列答案
相关题目
10.已知a,y满足$\left\{\begin{array}{l}{x-2≤0}\\{x-2y≤0}\\{x+2y-8≤0}\end{array}\right.$,则目标函数z=2x+y的最大值为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
14.某单位有职工200人,其年龄分布如下表:
为了解该单位职工的身体健康状况,用分层抽样的方法抽取一个容量为40的样本进行调查,则年龄在[30,40)内的职工应抽取的人数为18.
| 年龄(岁) | [20,30) | [30,40) | [40,60) |
| 人数 | 70 | 90 | 40 |
12.已知集合A={x|x2-x-2≤0},B={x|x2-1>0},则A∩B=( )
| A. | [-2,1) | B. | (-1,1) | C. | (1,2] | D. | (-2,-1)∪(1,2] |