题目内容
13.已知函数y=f(x)的图象为如图所示的折线ABC,则$\int_{-1}^1{[(x+1)f(x)]}$dx=( )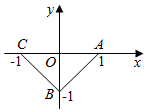
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
分析 先根据图象求出f(x)的表达式,在分段求出定积分.
解答 解:当0≤x≤1,f(x)=x-1,
当-1≤x<0时,f(x)=-x-1,
则$\int_{-1}^1{[(x+1)f(x)]}$dx=${∫}_{0}^{1}$(x+1)(x-1)dx+${∫}_{-1}^{0}$(x+1)(-x-1)dx=${∫}_{0}^{1}$(x2-1)dx-${∫}_{-1}^{0}$(x2+2x+1)dx=($\frac{1}{3}{x}^{3}-x$)|${\;}_{0}^{1}$-($\frac{1}{3}{x}^{3}+{x}^{2}+x$)|${\;}_{-1}^{0}$=$\frac{1}{3}$-1+(-$\frac{1}{3}$+1-1)=-1,
故选:D.
点评 本题考查了函数的解析式和定积分的计算,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
12.已知函数f(x)=$\left\{\begin{array}{l}{|lnx|,x>0}\\{|{x}^{2}+4x+3|,x≤0}\end{array}\right.$若关于x的方程f2(x)+bf(x)+4=0有8个不同的实数根,则实数b的取值范围是( )
| A. | [-$\frac{17}{4}$,-4)∪{-5} | B. | [-$\frac{13}{3}$,-4)∪{-5} | C. | [-5,-$\frac{13}{3}$] | D. | [-5,-4] |
5.设函数f(x)=$\left\{\begin{array}{l}{{2}^{x}+a,x>2}\\{lo{g}_{\frac{1}{2}}(\frac{9}{4}-x)+{a}^{2},x≤2}\end{array}\right.$,若f(x)的值域为R,则实数a的取值范围是( )
| A. | (-∞,-1]∪[2,+∞) | B. | [-1,2] | C. | (-∞,-2]∪[1,+∞) | D. | [-2,1] |
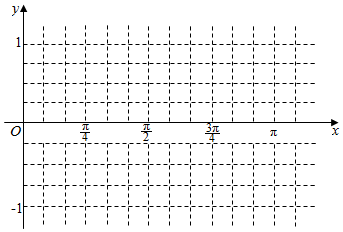 已知函数f(x)=$\frac{1}{2}$sinωx+$\frac{\sqrt{3}}{2}$cosωx(ω>0)的周期为π.
已知函数f(x)=$\frac{1}{2}$sinωx+$\frac{\sqrt{3}}{2}$cosωx(ω>0)的周期为π.