题目内容
M为抛物线y2=4x上一动点,F是焦点,P(5,4)是定点,则当|MP|+|MF|取最小值时点M的横坐标是( )
| A、2 | B、4 | C、6 | D、8 |
考点:抛物线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:设点M在准线上的射影为D,则根据抛物线的定义可知|MF|=|MD|进而把问题转化为求|MP|+|MD|取得最小,进而可推断出当D,M,P三点共线时|MP|+|MD|最小,答案可得.
解答:
解:设点M在准线上的射影为D,则根据抛物线的定义可知|MF|=|MD|
∴要求|MP|+|MF|取得最小值,即求|MP|+|MD|取得最小,
当D,M,P三点共线时|MP|+|MD|最小,为5-(-1)=6.
故选C.
∴要求|MP|+|MF|取得最小值,即求|MP|+|MD|取得最小,
当D,M,P三点共线时|MP|+|MD|最小,为5-(-1)=6.
故选C.
点评:本题考查抛物线的定义、标准方程,以及简单性质的应用,判断当D,M,P三点共线时|PM|+|MD|最小,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知b=-a2+3lna,d=c+2,则(a-c)2+(b-d)2的最小值为( )
A、
| ||
| B、2 | ||
C、2
| ||
| D、8 |
为了调查评价“中国好声音”栏目播出前后的电视台收视率有无明显提高,在播出前后分别从居民点抽取了100位居民,调查对“中国好声音”的关注情况,制成列联表,经过计算得K2的观测值k≈6.99,根据这一数据分析,下列说法正确的是( )
| A、有99%的人认为该栏目优秀 |
| B、有99%的人认为“中国好声音”栏目播出前后电视台的收视率有明显提高 |
| C、有99%的把握认为“中国好声音”栏目播出前后电视台的收视率有明显提高 |
| D、没有理由认为“中国好声音”栏目播出前后电视台的收视率有无明显提高 |
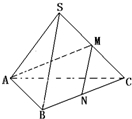 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
A、
| ||
| B、9π | ||
| C、12π | ||
| D、16π |
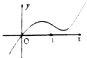 设R上的函数f(x)满足f(4)=1,它的导函数的图象如图,若正数a、b满足f(2a+b)<1,则
设R上的函数f(x)满足f(4)=1,它的导函数的图象如图,若正数a、b满足f(2a+b)<1,则| b+2 |
| a+2 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,-3) |
 如图,四棱锥V-ABCD的底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为
如图,四棱锥V-ABCD的底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为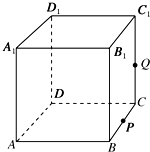 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是