题目内容
化简下列各式：
（1）sin（x+
）+2sin（x-
）-
cos（
-x）；
（2）
-2cos（α+β）．
（1）sin（x+
| π |
| 3 |
| π |
| 3 |
| 3 |
| 2π |
| 3 |
（2）
| sin(2α+β) |
| sinα |
考点：两角和与差的正弦函数,三角函数的化简求值
专题：三角函数的求值
分析：（1）根据两角和与差的正弦、余弦公式，以及特殊角的三角函数值对所求的式子化简求值；
（2）由角的特点将2α+β表示成（α+β）+α，再两角和与差的正弦公式对所求的式子化简．
（2）由角的特点将2α+β表示成（α+β）+α，再两角和与差的正弦公式对所求的式子化简．
解答：
解：（1）sin（x+
）+2sin（x-
）-
cos（
-x）
=sinxcos
+cosxsin
+2（sinxcos
-cosxsin
）-
（cos
cosx+sinxsin
）
=3sinxcos
-cosxsin
-
(cos
cosx+sinxsin
)
=
sinx-
cosx-
(-
cosx+
sinx)
=
sinx-
cosx+
cosx-
sinx=0；
（2）
-2cos（α+β）=
=
=
=
=
．
| π |
| 3 |
| π |
| 3 |
| 3 |
| 2π |
| 3 |
=sinxcos
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
=3sinxcos
| π |
| 3 |
| π |
| 3 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
=
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
（2）
| sin(2α+β) |
| sinα |
| sin[(α+β)+α]-2cos(α+β)sinα |
| sinα |
=
| sin(α+β)cosα+cos(α+β)sinα-2cos(α+β)sinα |
| sinα |
=
| sin(α+β)cosα-cos(α+β)sinα |
| sinα |
=
| sin(α+β-α) |
| sinα |
| sinβ |
| sinα |
点评：本题考查利用两角和与差的正弦、余弦公式，以及特殊角的三角函数值进行化简求值，注意角之间的关系，即变角的应用．
练习册系列答案
小题狂做系列答案
相关题目
在R上定义运算?：x?y=x（1-y），若不等式（x-a）?（x+a）＜1对任意实数x成立，则实数a的取值范围是（ ）
| A、{a|-1＜a＜1} | ||||
| B、{a|0＜a＜2} | ||||
C、{a|-
| ||||
D、{a|-
|
为了调查评价“中国好声音”栏目播出前后的电视台收视率有无明显提高，在播出前后分别从居民点抽取了100位居民，调查对“中国好声音”的关注情况，制成列联表，经过计算得K2的观测值k≈6.99，根据这一数据分析，下列说法正确的是（ ）
| A、有99%的人认为该栏目优秀 |
| B、有99%的人认为“中国好声音”栏目播出前后电视台的收视率有明显提高 |
| C、有99%的把握认为“中国好声音”栏目播出前后电视台的收视率有明显提高 |
| D、没有理由认为“中国好声音”栏目播出前后电视台的收视率有无明显提高 |
如图，四棱锥V-ABCD的底面ABCD是边长为2的正方形，其他四个侧面都是侧棱长为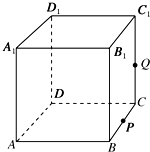
如图正方体ABCD-A1B1C1D1，棱长为1，P为BC中点，Q为线段CC1上的动点，过A、P、Q的平面截该正方体所得的截面记为S，则下列命题正确的是