题目内容
已知函数f(x)=
sinωx+cosωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的一条对称轴是( )
| 3 |
A、x=-
| ||
B、x=
| ||
C、x=-
| ||
D、x=
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:化简函数f(x)=
sinωx+cosωx为f(x)=2sin(ωx+
),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,求出函数的周期,推出ω,得到函数解析式,从而可求f(x)的一条对称轴.
| 3 |
| π |
| 6 |
解答:
解:函数f(x)=
sinωx+cosωx=2sin(ωx+
),
因为y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,函数的周期T=π,
所以ω=2,所以f(x)=2sin(2x+
),
因为2x+
=
+kπ k∈Z,
解得x=
+
,k∈Z,
当k=0时,有x=
.
故选:D.
| 3 |
| π |
| 6 |
因为y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,函数的周期T=π,
所以ω=2,所以f(x)=2sin(2x+
| π |
| 6 |
因为2x+
| π |
| 6 |
| π |
| 2 |
解得x=
| kπ |
| 2 |
| π |
| 6 |
当k=0时,有x=
| π |
| 6 |
故选:D.
点评:本题主要考察了两角和与差的正弦函数公式的应用,考察了由y=Asin(ωx+φ)的部分图象确定其解析式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆O:x2+y2=4,过点M(1,
)的两条弦AC,BD互相垂直,则AC+BD的最大值是( )
| 2 |
| A、6 | ||
B、2
| ||
C、4
| ||
D、5
|
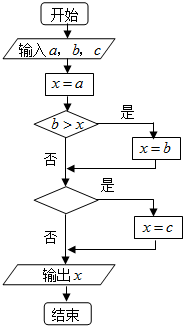 如图的程序框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( )
如图的程序框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( )| A、c>x | B、x>a |
| C、c>b | D、b>c |
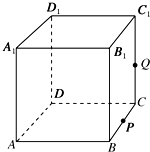 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是