题目内容
已知函数f(x)=
x3+ax2+b,其中a,b∈R.
(1)若曲线y=f(x)在点(-1,f(-1))处的切线方程是3x+y+2=0,求a、b的值;
(2)若b=
,且关于x的方程f(x)=0有两个不同的正实数根,求实数a的取值范围.
| 1 |
| 3 |
(1)若曲线y=f(x)在点(-1,f(-1))处的切线方程是3x+y+2=0,求a、b的值;
(2)若b=
| 9 |
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,导数的综合应用
分析:(1)求出导数,求出切线的斜率和切点,得到a,b的方程,解得即可;
(2)由于f(0)=b=
>0,关于x的方程f(x)=0有两个不同的正实数根,则有f(x)的极小值为负即可,通过导数的符号即可确定极小值点,解不等式即可得到.
(2)由于f(0)=b=
| 9 |
| 2 |
解答:
解:(1)函数f(x)=
x3+ax2+b的导数f′(x)=x2+2ax,
则在点(-1,f(-1))处的切线斜率为:f′(-1)=1-2a,
由于在点(-1,f(-1))处的切线方程是3x+y+2=0,则1-2a=-3,
解得a=2,
又切点为(-1,1),则-
+2+b=1,
解得b=-
;
(2)函数f(x)=
x3+ax2+b的导数,
f′(x)=x2+2ax,
由于f(0)=b=
>0,
关于x的方程f(x)=0有两个不同的正实数根,
则有f(x)的极小值为负即可.
由f′(x)=x2+2ax=x(x+2a),
则0<x<-2a,f′(x)<0,x<0或x>-2a,f′(x)>0,
则有a<0,且f(-2a)<0,
即有a<0,且
×(-8a3)+4a3+
<0,
解得,a<-
.
故实数a的取值范围是(-∞,-
).
| 1 |
| 3 |
则在点(-1,f(-1))处的切线斜率为:f′(-1)=1-2a,
由于在点(-1,f(-1))处的切线方程是3x+y+2=0,则1-2a=-3,
解得a=2,
又切点为(-1,1),则-
| 1 |
| 3 |
解得b=-
| 2 |
| 3 |
(2)函数f(x)=
| 1 |
| 3 |
f′(x)=x2+2ax,
由于f(0)=b=
| 9 |
| 2 |
关于x的方程f(x)=0有两个不同的正实数根,
则有f(x)的极小值为负即可.
由f′(x)=x2+2ax=x(x+2a),
则0<x<-2a,f′(x)<0,x<0或x>-2a,f′(x)>0,
则有a<0,且f(-2a)<0,
即有a<0,且
| 1 |
| 3 |
| 9 |
| 2 |
解得,a<-
| 3 |
| 2 |
故实数a的取值范围是(-∞,-
| 3 |
| 2 |
点评:本题考查导数的运用:求切线方程、求极值,考查判断能力和运算能力,属于中档题和易错题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知函数 f(x)=
,则f[f(4)]=( )
|
A、
| ||
B、
| ||
C、
| ||
| D、4 |
下列命题正确的是( )
①
=
②已知非零向量
,
,若
•
=0,则
=2
③(1+x+x2)(x-
)6的展开式中的常数项为-5.
④已知(
+
)n展开式中常数项是
,则n=12.
⑤抛掷两枚骰子,当至少有一枚4点或5点出现时,就说这次实验成功,则在30次实验中成功次数X的方差D(X)=
.
①
| 2cos5°-sin25° |
| cos25° |
| 3 |
②已知非零向量
| a |
| b |
| a |
| b |
|
| ||||
|
|
③(1+x+x2)(x-
| 1 |
| x |
④已知(
| x |
| 1 |
| x |
| C | 4 n |
⑤抛掷两枚骰子,当至少有一枚4点或5点出现时,就说这次实验成功,则在30次实验中成功次数X的方差D(X)=
| 200 |
| 27 |
| A、①③④ | B、②④⑤ |
| C、①④⑤ | D、①③⑤ |
在R上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对任意实数x成立,则实数a的取值范围是( )
| A、{a|-1<a<1} | ||||
| B、{a|0<a<2} | ||||
C、{a|-
| ||||
D、{a|-
|
若函数f(x),g(x)分别是定义在实数集R上的奇函数、偶函数,且满足f(x)-g(x)=ex(e是自然对数的底数),则有( )
| A、f(2)<f(3)<g(0) |
| B、g(0)<f(3)<f(2) |
| C、g(0)<f(2)<f(3) |
| D、f(2)<g(0)<f(3) |
已知b=-a2+3lna,d=c+2,则(a-c)2+(b-d)2的最小值为( )
A、
| ||
| B、2 | ||
C、2
| ||
| D、8 |
已知(2,1)是直线l被椭圆
+
=1所截得的线段的中点,则直线l的方程是( )
| x2 |
| 16 |
| y2 |
| 4 |
| A、x+2y-4=0 |
| B、x-2y=0 |
| C、x+8y-10=0 |
| D、x-8y+6=0 |
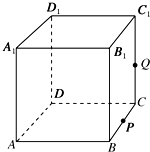 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是