题目内容
已知二次函数f(x)=ax2+bx+c(a≠0)(a,b,c∈R),且同时满足下列条件:①f(-1)=0;②对任意实数x,都有f(x)-x≥0;③当x∈(0,2)时,有f(x)≤(
)2.
(1)求f(1);
(2)求a,b,c的值;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调函数,求m的取值范围.
| x+1 |
| 2 |
(1)求f(1);
(2)求a,b,c的值;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调函数,求m的取值范围.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)令x=1,有f(1)-1≥0和f(1)≤(
)2=1,求出f(1);
(2)由f(-1)=0,得a-b+c=0,①由f(1)=1得a+b+c=1②
联立①②可得b=a+c=
,再由f(x)-x≥0,即ax2+(a+c)x+c-x≥0,约束可得结果.
(3)把第(1)、(2)问的结果代入g(x),得出对称轴方程,由二次函数的单调性可求.
| 1+1 |
| 2 |
(2)由f(-1)=0,得a-b+c=0,①由f(1)=1得a+b+c=1②
联立①②可得b=a+c=
| 1 |
| 2 |
(3)把第(1)、(2)问的结果代入g(x),得出对称轴方程,由二次函数的单调性可求.
解答:
解:(1)由f(-1)=0,得a-b+c=0,①
令x=1,有f(1)-1≥0和f(1)≤(
)2=1,
∴f(1)=1.
(2)由f(1)=1得a+b+c=1②
联立①②可得b=a+c=
,
由题意知,对任意实数x,都有f(x)-x≥0,即ax2+(a+c)x+c-x≥0,
即ax2-
x+c≥0对任意实数x恒成立,于是
,即
,
∵c=
-a,
∴
⇒
,
∴2a-
=0,∴a=
∴c=
-a=
,
∴a=c=
,b=
.
(3)由(2)得:g(x)=f(x)-mx=
x2+
x+
-mx=
[x2+(2-4m)x+1]
此抛物线的对称轴方程为x=-
∵x∈[-1,1]时,g(x)是单调的,
∴|-
|≥1,解得m≤0或m≥1.
∴m的取值范围是(-∞,0]∪[1,+∞).
令x=1,有f(1)-1≥0和f(1)≤(
| 1+1 |
| 2 |
∴f(1)=1.
(2)由f(1)=1得a+b+c=1②
联立①②可得b=a+c=
| 1 |
| 2 |
由题意知,对任意实数x,都有f(x)-x≥0,即ax2+(a+c)x+c-x≥0,
即ax2-
| 1 |
| 2 |
|
|
∵c=
| 1 |
| 2 |
∴
|
|
∴2a-
| 1 |
| 2 |
| 1 |
| 4 |
∴c=
| 1 |
| 2 |
| 1 |
| 4 |
∴a=c=
| 1 |
| 4 |
| 1 |
| 2 |
(3)由(2)得:g(x)=f(x)-mx=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
此抛物线的对称轴方程为x=-
| 2-4m |
| 2 |
∵x∈[-1,1]时,g(x)是单调的,
∴|-
| 2-4m |
| 2 |
∴m的取值范围是(-∞,0]∪[1,+∞).
点评:本题主要考查二次函数的有关性质,利用二次函数的对称轴、单调性解题是关键.

练习册系列答案
相关题目
若函数f(x),g(x)分别是定义在实数集R上的奇函数、偶函数,且满足f(x)-g(x)=ex(e是自然对数的底数),则有( )
| A、f(2)<f(3)<g(0) |
| B、g(0)<f(3)<f(2) |
| C、g(0)<f(2)<f(3) |
| D、f(2)<g(0)<f(3) |
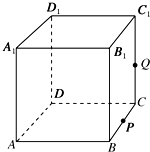 如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是
如图正方体ABCD-A1B1C1D1,棱长为1,P为BC中点,Q为线段CC1上的动点,过A、P、Q的平面截该正方体所得的截面记为S,则下列命题正确的是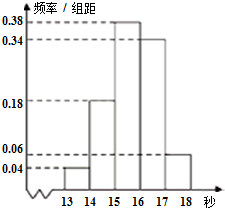 高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.