题目内容
求下列关于x的不等式的解集：
（1）-x2+7x＞6；
（2）x2-（2m+1）x+m2+m＜0．
（1）-x2+7x＞6；
（2）x2-（2m+1）x+m2+m＜0．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：利用一元二次不等式的解法即可得出．
解答：
解：（1）∵-x2+7x＞6，
∴-x2+7x-6＞0，
∴x2-7x+6＜0，
∴（x-1）（x-6）＜0，解得1＜x＜6，
即不等式的解集是{x|1＜x＜6}．
（2）x2-（2m+1）x+m2+m＜0，因式分解得（x-m）[x-（m+1）]＜0．
∵m＜m+1，∴m＜x＜m+1．
因此不等式的解集为{x|m＜x＜m+1}．
∴-x2+7x-6＞0，
∴x2-7x+6＜0，
∴（x-1）（x-6）＜0，解得1＜x＜6，
即不等式的解集是{x|1＜x＜6}．
（2）x2-（2m+1）x+m2+m＜0，因式分解得（x-m）[x-（m+1）]＜0．
∵m＜m+1，∴m＜x＜m+1．
因此不等式的解集为{x|m＜x＜m+1}．
点评：本题考查了一元二次不等式的解法，属于基础题．
练习册系列答案
相关题目
若圆（x-a）2+（y-b）2=b2+1始终平分圆（x+1）2+（y+1）2=4的周长，则a，b满足的关系是（ ）
| A、a2+2a+2b-3=0 |
| B、a2+b2+2a+2b+5=0 |
| C、a2+2a+2b+5=0 |
| D、a2-2a-2b+5=0 |
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜
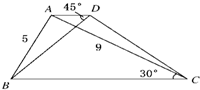如图所示，在梯形ABCD中，AD∥BC，AB=5，AC=9，∠BCA=30°，∠ADB=45°．则BD的长为