题目内容
已知复数z1=2-2i，且|z|=1，则|z-z1|的最大值为 ．
考点：复数求模
专题：数系的扩充和复数
分析：由题意可得|z-z1|表示单位圆上的点与点A（2，-2）间的距离，故它的最大值为|AO|+1，计算求得结果
解答：
解：复数z1=2-2i在负平面内对应点A（2，-2），
满足|z|=1的复数z对应点在以原点O为圆心的单位圆上，
而|z-z1|表示单位圆上的点与点A间的距离，故它的最大值为|AO|+1=
+1=2
+1，
故答案为：2
+1．
满足|z|=1的复数z对应点在以原点O为圆心的单位圆上，
而|z-z1|表示单位圆上的点与点A间的距离，故它的最大值为|AO|+1=
| 4+4 |
| 2 |
故答案为：2
| 2 |
点评：本题主要考查复数的代数表示及其几何意义，复数与复平面内对应点之间的关系，属于基础题．
练习册系列答案
相关题目
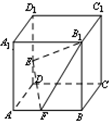（理科）已知如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为棱DD1，AB上的点（不含顶点）．则下列说法正确的是