题目内容
已知数列{an}中,a1=2,且
=
,则an= .
| an |
| an-1 |
| n-1 |
| n+1 |
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:利用累乘法即可求得an,注意检验n=1时情形.
解答:
解:∵a1=2,且
=
,
∴n≥2时,an=a1•
•
•
…
=2•
•
•
…
•
•
=2•
=
,
又a1=2适合上式,
∴an=
,
故答案为:
.
| an |
| an-1 |
| n-1 |
| n+1 |
∴n≥2时,an=a1•
| a2 |
| a1 |
| a3 |
| a2 |
| a4 |
| a3 |
| an |
| an-1 |
=2•
| 1 |
| 3 |
| 2 |
| 4 |
| 3 |
| 5 |
| n-3 |
| n-1 |
| n-2 |
| n |
| n-1 |
| n+1 |
=2•
| 2 |
| n(n+1) |
| 4 |
| n(n+1) |
又a1=2适合上式,
∴an=
| 4 |
| n(n+1) |
故答案为:
| 4 |
| n(n+1) |
点评:该题考查由数列递推式求数列通项,属基础题,注意掌握累乘法的递推式特征:
=f(n).
| an+1 |
| an |

练习册系列答案
相关题目
 在平行六面休ABCD-A′B′C′D′中,若
在平行六面休ABCD-A′B′C′D′中,若| AC′ |
| AB |
| BC |
| C′C |
A、
| ||
B、
| ||
C、
| ||
D、
|
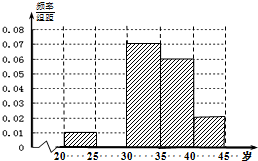 对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:
对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得: