题目内容
对于任意的x1,x2∈(0,+∞),若函数f(x)=lgx,满足
≤f(
),运用类比的思想方法,当x1,x2∈(
,π)时,试比较
与cos
的大小关系 .
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| π |
| 2 |
| cosx1+cosx2 |
| 2 |
| x1+x2 |
| 2 |
考点:类比推理
专题:规律型,函数的性质及应用,推理和证明
分析:由类比推理的规则得出结论,本题中所用来类比的函数是一个变化率越来越大的函数,而要研究的函数是一个变化率越来越小的函数,其类比方式可得答案.
解答:
解:由题意变化率逐渐变大的函数有线段AB总是位于A、B两点之间函数图象的下方,因此有结论
≤f(
)成立
函数y=cosx(x∈(
,π))变化率逐渐变小,函数有线段AB总是位于A、B两点之间函数图象的上方,故可类比得到结论
≥cos
,
故答案为:
≥cos
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
函数y=cosx(x∈(
| π |
| 2 |
| cosx1+cosx2 |
| 2 |
| x1+x2 |
| 2 |
故答案为:
| cosx1+cosx2 |
| 2 |
| x1+x2 |
| 2 |
点评:本题考查类比推理,求解本题的关键是理解类比的定义,及本题类比的对象之间的联系与区别,从而得出类比结论

练习册系列答案
相关题目
一个算法的程序框图如图,则其输出结果是( )
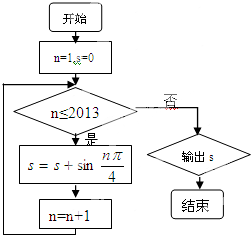

| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|