题目内容

在△ABC中，已知sinA=2sinBcosC，且a2+b2-ab=c2，则三角形的形状为
 
．
考点：余弦定理,正弦定理
专题：计算题,解三角形
分析：由sinA=2sinBcosC，得sin（B+C）=2sinBcosC，展开化简可得B=C；由a2+b2-ab=c2，利用余弦定理可求得C，综上可得结论．
解答： 解：由sinA=2sinBcosC，得
sin（B+C）=2sinBcosC，即sinBcosC+cosBsinC=2sinBcosC，
∴sin（B-C）=0，
∴B=C，
a2+b2-ab=c2，可化为a2+b2-c2=ab，则
a2+b2-c2
2ab
=
1
2
，
∴cosC=
1
2
，C=60°，B=60°，
综上知△ABC为等边三角形，
故答案为：等边三角形．
点评：该题考查正弦定理、余弦定理及其应用，属基础题．
练习册系列答案
相关题目
在△ABC中，已知
cosA
cosB
=
a
b
，则△ABC的形状为
 
．
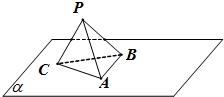已知三棱锥P-ABC的侧面PAC⊥底面ABC，侧棱PA⊥AB，且PA=PC=AC=AB=4．如图AB?平面α，以直线AB为轴旋转三棱锥，记该三棱锥在平面α上的俯视图面积为S，则S的最小值是
 
，S的最大值是
 
．
若实数x，y满足不等式组
x≥1
y≥1
x+2y≤5
则
y
x
的最大值是
 
．
已知在半径为4的球面上有A、B、C、D四个点，且AB=CD=4，则四面体ABCD体积的最大值为
 
．
已知函数f（x）=x2sinx，各项均不相等的有限项数列{xn}的各项xi满足|xi|≤1．令F（n）=
n
i=1
x1•
n
i=1
f(xi)，n≥3且n∈N，例如：F（3）=（x1+x2+x3）•（f（x1）+f（x2）+f（x3））．
下列给出的结论中：
①存在数列{xn}使得F（n）=0；
②如果数列{xn}是等差数列，则F（n）＞0；
③如果数列{xn}是等比数列，则F（n）＞0；
正确结论的序号是
 
．
对于函数y=f（x），若在其定义域内存在x0，使得x0f（x0）=1成立，则称函数f（x）具有性质P．
（1）下列函数中具有性质P的有
 

①f（x）=-2x+2
2

②f（x）=sinx（x∈[0，2π]）
③f（x）=x+
1
x
，（x∈（0，+∞））
（2）若函数f（x）=alnx具有性质P，则实数a的取值范围是
 
．
对于任意的x1，x2∈（0，+∞），若函数f（x）=lgx，满足
f(x1)+f(x2)
2
≤f（
x1+x2
2
），运用类比的思想方法，当x1，x2∈（
π
2
，π）时，试比较
cosx1+cosx2
2
与cos
x1+x2
2
的大小关系
 
．
参数方程
x=cosθ
y=1+cosθ
（θ为参数）表示的曲线是（　　）
A、圆B、直线C、线段D、射线

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网