题目内容
10.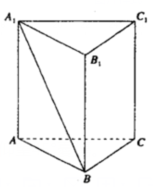 如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,侧棱AA1⊥面ABC,若AB=AA1,则直线A1B与AC所成角的余弦值为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,侧棱AA1⊥面ABC,若AB=AA1,则直线A1B与AC所成角的余弦值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{14}}{2}$ | D. | $\frac{\sqrt{14}}{4}$ |
分析 由题意,底面ABC为正三角形,侧棱AA1⊥面ABC,通过补形将三棱柱ABC-A1B1C1的转化为长方体,找到直线A1B与AC所成角平面角,利用余弦定理求解.
解答 解:底面ABC为正三角形,侧棱AA1⊥面ABC,过B,C点分别作AC,AB的平行线交于F,同理,作过B1,C1点分别作A1B,A1C1的平行线交于E,连接EF,可得ABCF-A1B1C1E为长方体.底面是菱形.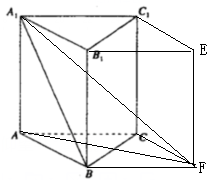
∴AC∥BF,
故直线A1B与AC所成角即为∠A1BF(或补角)
∵底面ABC为正三角形,设AB═AC=AA1=a,则A1B=$\sqrt{2}a$,
AF=$\sqrt{3}a$,A1F=$\sqrt{{A}_{1}{A}^{2}+A{F}^{2}}=2a$.
那么|cos∠A1BF|=|$\frac{{A}_{1}{B}^{2}+B{F}^{2}-{{A}_{1}F}^{2}}{2{A}_{1}B•BF}$|=$\frac{\sqrt{2}}{4}$
故选B.
点评 本题考查两条异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
18.在等差数列{an}中,若a3=9,a6=15,则a12等于( )
| A. | 3 | B. | 12 | C. | 27 | D. | 36 |
5.已知sinα+cosα=-$\sqrt{2}$,则tanα+$\frac{1}{tanα}$的值等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
15.函数y=cos2x,x∈R的最小正周期为( )
| A. | 2 | B. | π | C. | 2π | D. | $\frac{1}{π}$ |
2.直线l1:2x-y-1=0与直线l2:mx+y+1=0互相垂直的充要条件是( )
| A. | m=-2 | B. | m=-$\frac{1}{2}$ | C. | m=$\frac{1}{2}$ | D. | m=2 |
19.已知向量$\overrightarrow{a}$=(5,2),$\overrightarrow{b}$=(1,6),则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为( )
| A. | (4,-4) | B. | (6,8) | C. | (5,12) | D. | (3,11) |
2.已知曲线y=lnx的切线过原点,则此切线的斜率为( )
| A. | e | B. | -e | C. | $\frac{1}{e}$ | D. | -$\frac{1}{e}$ |