题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{e^{-x}}-2,x≤0\\ 2ax-1,x>0\end{array}$(a>0),对于下列命题:(1)函数f(x)的最小值是-1;
(2)函数f(x)在R上是单调函数;
(3)若f(x)>0在($\frac{1}{2}$,+∞)上恒成立,则a的取值范围是a>1,
其中真命题的序号是(1).
分析 画出图象,根据图象判定(1),(2),对于(3)由图象说明函函数f(x)在($\frac{1}{2}$,+∞)上是单调增函数,f(x)min>0即可,
即f($\frac{1}{2}$)≥0解,得a的取值范围是a≥1;
解答 解:对于(1),由图只需说明在点x=0处函数f(x)的最小值是-1;故正确;
对于(2),由图象说明函函数f(x)在R上不是单调函数;故错;
对于(3)由图象说明函函数f(x)在($\frac{1}{2}$,+∞)上是单调增函数,f(x)min>0即可,
即 f($\frac{1}{2}$)≥0解,得a的取值范围是a≥1;故错;
f($\frac{1}{2}$)≥0解,得a的取值范围是a≥1;故错;
答案为:(1)
点评 利用函数的图象研究函数的单调区间以及根据函数的增减性得到函数的最值是常用的方法,解答本题的关键是图象法

练习册系列答案
相关题目
15.函数y=cos2x,x∈R的最小正周期为( )
| A. | 2 | B. | π | C. | 2π | D. | $\frac{1}{π}$ |
16.已知函数f(x)=x3-x+3,则曲线y=f(x)在点(1,f(1))处的切线方程为( )
| A. | 2x-y+1=0 | B. | x-2y+1=0 | C. | 2x+y+1=0 | D. | 2x-y+2=0 |
13. 已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
 已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 0 |
2.已知曲线y=lnx的切线过原点,则此切线的斜率为( )
| A. | e | B. | -e | C. | $\frac{1}{e}$ | D. | -$\frac{1}{e}$ |
19.函数f(x)=$\frac{1}{{\sqrt{x-2}}}$的定义域为( )
| A. | (-∞,2)∪(2,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (-∞,2) |
16.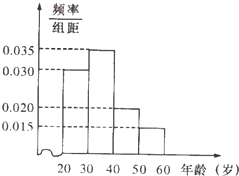 某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.
某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求四个年龄段应分别抽取的人数;
(2)根据频率分布直方图,估计全厂工人的平均年龄;
(3)随机从年龄段[20,30)和[40,50)中各抽取1人,设这两人中AB两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望.
 某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.
某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 27 | 16 |
| [30,40) | 28 | 18 |
| [40,50) | 26 | 9 |
| [50,60] | 6 | 4 |
(2)根据频率分布直方图,估计全厂工人的平均年龄;
(3)随机从年龄段[20,30)和[40,50)中各抽取1人,设这两人中AB两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望.