题目内容
已知Sn是等差数列{an}(n∈N*)的前n项和,且S6>S7>S5,有下列五个命题:
①d<0;
②S11>0;
③S12<0;
④数列{Sn}中的最大项为S11;
⑤|a6|>|a7|.
其中正确的命题是 (写出你认为正确的所有命题的序号)
①d<0;
②S11>0;
③S12<0;
④数列{Sn}中的最大项为S11;
⑤|a6|>|a7|.
其中正确的命题是
考点:等差数列的性质
专题:等差数列与等比数列
分析:先由条件确定第六项和第七项的正负,进而确定公差的正负,再将S11,S12由第六项和第七项的正负判定,结合a6>0,a7<0,且a6+a7>0判断⑤.
解答:
解:由题可知等差数列为an=a1+(n-1)d,
由s6>s7有s6-s7>0,即a7<0,
由s6>s5同理可知a6>0,
则a1+6d<0,a1+5d>0,
由此可知d<0 且-5d<a1<-6d.
∵Sn=na1+
,
∴s11=11a1+55d=11(a1+5d)>0,
s12=12a1+66d=12(a1+a12)=12(a6+a7),
∵S7>S5,∴S7-S5=a6+a7>0,
∴s12>0.
由a6>0,a7<0,且a6+a7>0,
可知|a6|>|a7|.
即①②⑤是正确的,③④是错误的.
故答案为:①、②、⑤.
由s6>s7有s6-s7>0,即a7<0,
由s6>s5同理可知a6>0,
则a1+6d<0,a1+5d>0,
由此可知d<0 且-5d<a1<-6d.
∵Sn=na1+
| n(n-1)d |
| 2 |
∴s11=11a1+55d=11(a1+5d)>0,
s12=12a1+66d=12(a1+a12)=12(a6+a7),
∵S7>S5,∴S7-S5=a6+a7>0,
∴s12>0.
由a6>0,a7<0,且a6+a7>0,
可知|a6|>|a7|.
即①②⑤是正确的,③④是错误的.
故答案为:①、②、⑤.
点评:本题主要考查等差数列的前n项和公式的应用,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
若执行如图的程序框图,输出S的值为4,则判断框中应填入的条件是( )
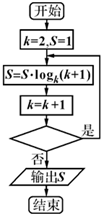

| A、k<14? |
| B、k<15? |
| C、k<16? |
| D、k<17? |
已知实数x、y满足
,则z=(x-1)2+(y-2)2的最小值为( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数y=sin(2x+ϕ)的图象沿x轴向左平移
个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为( )
| π |
| 8 |
A、
| ||
B、
| ||
| C、0 | ||
D、-
|
设集合A={{x|y=
},集合B={x||x-2|<2},则A∩B等于( )
| 2+x-x2 |
| A、(0,2] | B、[0,2] |
| C、[-1,2) | D、∅ |