题目内容
函数f（x）=2sin（
x）-log2x的零点个数为（ ）
| 5π |
| 8 |
| A、1 | B、2 | C、3 | D、4 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：本题将函数的零点问题转化为两条曲线的交点个数，通过曲线的图形情况研究，进而判断函数的零点个数，得到本题结论．
解答：
解：∵函数f（x）=2sin（
x）-log2x，
∴令f（x）=0，则有：2sin（
x）=log2x．
下面研究函数y=2sin（
x）与函数y=log2x的图象，
函数y=2sin（
x）周期为T=2π×
=
，过点（4，2），
函数y=log2x过点（1，0），（4，2），在（0，+∞）上单调递增，
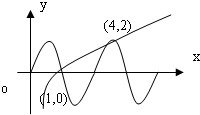
如图可知，函数y=2sin（
x）与函数y=log2x的图象有三个公共点，
∴函数f（x）=2sin（
x）-log2x的零点个数为3．
故选C．
| 5π |
| 8 |
∴令f（x）=0，则有：2sin（
| 5π |
| 8 |
下面研究函数y=2sin（
| 5π |
| 8 |
函数y=2sin（
| 5π |
| 8 |
| 8 |
| 5π |
| 16 |
| 5 |
函数y=log2x过点（1，0），（4，2），在（0，+∞）上单调递增，
如图可知，函数y=2sin（
| 5π |
| 8 |
∴函数f（x）=2sin（
| 5π |
| 8 |
故选C．
点评：本题考查了零点个数与函数图象特征，本题难度不大，属于基础题．
练习册系列答案
相关题目
设a=2
，b=log32，c=cos100°，则（ ）
| 1 |
| 3 |
| A、c＞b＞a |
| B、a＞c＞b |
| C、c＞a＞b |
| D、a＞b＞c |
f（x）=
则f[f（
）]=（ ）
|
| 1 |
| 9 |
| A、-2 | ||
| B、-3 | ||
| C、9 | ||
D、
|
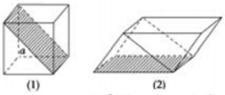如图（1）所示，已知正方体面对角线长为a，沿阴影面将它切割成两块，拼成如图（2）所示的几何体，那么此几何体的表面积为（ ）A、（1+2
| ||
B、（2+
| ||
C、（3+2
| ||
D、（4+
|