题目内容
13.某篮球队规定,在一轮训练中,每人最多可投篮4次,一旦投中即停止该轮训练,否则一直试投到第四次为止.已知一个投手的投篮命中概率为$\frac{3}{4}$,(Ⅰ)求该选手投篮3次停止该轮训练的概率;
(Ⅱ)求一轮训练中,该选手的实际投篮次数ξ的概率分布和数学期望.
分析 (Ⅰ)该选手投篮3次停止该轮训练即第三次投中事件为A,由相互独立事件乘法概率公式能求出该选手投篮3次停止该轮训练的概率.
(Ⅱ)由题意ξ的可能取值为1、2、3、4,分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
解答 解:(Ⅰ)该选手投篮3次停止该轮训练即第三次投中事件为A,
概率为P(A)=(1-$\frac{3}{4}$)2•$\frac{3}{4}$=$\frac{3}{64}$.(4分)
(Ⅱ)由题意ξ的可能取值为1、2、3、4,(5分)
P(ξ=1)=$\frac{3}{4}$,
P(ξ=2)=(1-$\frac{3}{4}$)$•\frac{3}{4}$=$\frac{3}{16}$,
P(ξ=3)=(1-$\frac{3}{4}$)2•$\frac{3}{4}$=$\frac{3}{64}$,
P(ξ=4)=(1-$\frac{3}{4}$)3$•\frac{3}{4}$+(1-$\frac{3}{4}$)4=$\frac{1}{64}$,(11分)
∴ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{3}{4}$ | $\frac{3}{16}$ | $\frac{3}{64}$ | $\frac{1}{64}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
3.在空间中,“直线a,b没有公共点”是“直线a,b互为异面直线”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8. 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示,则此几何体的表面积是( )| A. | 24π | B. | $24π+8\sqrt{2}π$ | C. | $24π+4\sqrt{2}π$ | D. | 32π |
18.从1,2,3,4,5,6,7这7个数字中,任取2个数字相加,其和为偶数的概率是( )
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{8}{21}$ |
5.某企业生产A、B两种产品,现有资源如下:煤360吨,水300吨,电200千瓦.每生产1吨A产品需消耗煤9吨,水3吨,电4千瓦,利润7万元;每生产1吨B产品需消耗煤4吨,水10吨,电5千瓦,利润12万元.
(Ⅰ)根据题目信息填写下表:
(Ⅱ)设分别生产A、B两种产品x吨、y吨,总产值为z万元,请列出x、y满足的不等式组及目标函数.
(Ⅲ)试问该企业利用现有资源,生产A、B两种产品各多少吨,才能获得最大利润?
(Ⅰ)根据题目信息填写下表:
| 每吨产品 | 煤(吨) | 水(吨) | 电(千瓦) |
| A | |||
| B |
(Ⅲ)试问该企业利用现有资源,生产A、B两种产品各多少吨,才能获得最大利润?
2.在△ABC中,角A,B,C所对的边分别为a,b,c,若$\frac{a}{b}=2cosC$,则△ABC的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
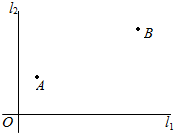 如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.
如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$. 已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.
已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.