题目内容
4.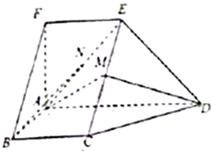 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.(1)证明:平面AMD⊥平面CDE;
(2)证明:BN∥平面CDE.
分析 (1)欲证平面AMD⊥平面CDE,即证CE⊥平面AMD,根据线面垂直的判定定理可知只需证CE与平面AMD内两相交直线垂直即可,易证DM⊥CE,MP⊥CE;
(2)取DE的中点Q,连接NQ,CQ,证明BCQN是平行四边形,所以BN∥CQ,利用线面平行的判定定理,即可证明BN∥平面CDE.
解答 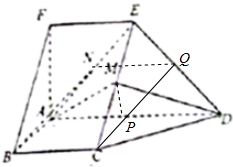 证明:(1)因为DC=DE且M为CE的中点,
证明:(1)因为DC=DE且M为CE的中点,
所以DM⊥CE.
设P为AD的中点,连接MP,则MP⊥CE.
又MP∩DM=M,
故CE⊥平面AMD.而CE?平面CDE,
所以平面AMD⊥平面CDE;
(2)取DE的中点Q,连接NQ,CQ,则NQ平行且等于$\frac{1}{2}$AD,
因为AD∥BC,BC=$\frac{1}{2}$AD,
所以NQ平行且等于BC,
所以BCQN是平行四边形,
所以BN∥CQ,
因为BN?平面CDE,CQ?平面CDE,
所以BN∥平面CDE.
点评 本题考查了线面平行,面面垂直的判定,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.已知集合A={x∈R|-1<x<3},B={x∈R|-1<x<m+1},若x∈B成立的一个充分不必要条件是x∈A,则实数m的取值范围是( )
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | -2<m<2 |
9.随机变量ξ的分布列如表,则D(ξ)=$\frac{5}{9}$
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | p |
14.复数$\frac{5}{2-i}$的共轭复数是( )
| A. | 2+i | B. | -2+i | C. | -2-i | D. | 2-i |