复数$\frac{5}{2-i}$的共轭复数是( )A．2+iB．-2+iC．-2-iD．2-i 题目和参考答案——青夏教育精英家教网—

题目内容

14．复数$\frac{5}{2-i}$的共轭复数是（　　）

A．

2+i

B．

-2+i

C．

-2-i

D．

2-i

分析利用复数代数形式的乘除运算化简，然后利用共轭复数的概念得答案．

解答解：∵$\frac{5}{2-i}$=$\frac{5（2+i）}{（2-i）（2+i）}=\frac{5（2+i）}{5}=2+i$，
∴复数$\frac{5}{2-i}$的共轭复数是2-i．
故选：D．

点评本题考查复数代数形式的乘除运算，考查了共轭复数的概念，是基础题．

练习册系列答案

相关题目

4．

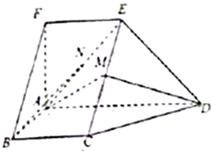如图，在五面体ABCDEF中，FA⊥平面ABCD，AD∥BC∥FE，AB⊥AD，M为EC的中点，N为AE的中点，AF=AB=BC=FE=$\frac{1}{2}$AD．
（1）证明：平面AMD⊥平面CDE；
（2）证明：BN∥平面CDE．

5．等边△ABC的边长为2，则$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影为（　　）

2．按如图所示的算法流程图运算，若输出k=2，则输入x的取值范围是（　　）

9．

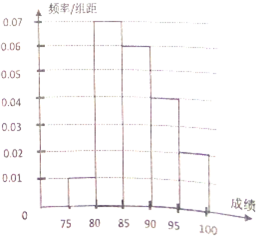2016高考成绩已经揭晓，各大985名校展开争抢优秀生源的大战．某校在参加“华约”联盟笔试的学生中随机抽取100名学生，将他们的成绩由低到高分成1～5组得到如图的频率频率分布直方图．
（Ⅰ）估计参加“华约”联盟笔试成绩的中位数（结果精确到个位）；
（Ⅱ）若在成绩较高的第4，5组中用分层抽样抽取6名学生进入模拟面试，求第4，5组各抽取多少人？
（Ⅲ）在（Ⅱ）的条件下，从这6名学生中任取2人参加答辩环节，求这两人来自同一组的概率．

19．设L为曲线C：y=$\frac{lnx}{x}$在点（1，0）处的切线．
（1）求L的方程；
（2）证明：f（x）≤x-1在定义域内恒成立．

1．已知角α、β的顶点与坐标原点重合，始边与x轴的非负半轴重合，点P（1，$\sqrt{3}$）、Q（3，-4）分别在角α、β的终边上，则sin（α-β）的值为（　　）

A．

$\frac{3\sqrt{3}-4}{10}$

B．

$\frac{3\sqrt{3}+4}{10}$

C．

$\frac{3+4\sqrt{3}}{10}$

D．

$\frac{3-4\sqrt{3}}{10}$

18．求下列函数的极值：y=x⁴-8x²+2．

19．设f（x）是定义在R上的奇函数，当x＞0时，f′（x）sinx+f（x）cosx＞0且f（$\frac{π}{2}$）=1，则f（x）sinx≤1的整数解的集合为{-1，0，1}．

试题分类