题目内容
9.随机变量ξ的分布列如表,则D(ξ)=$\frac{5}{9}$| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | p |
分析 利用分布列的性质求出a,然后直接使用公式求期望、方差.
解答 解:由题意可知$\frac{1}{2}+\frac{1}{3}+p=1$,解得p=$\frac{1}{6}$.
Eξ=0×$\frac{1}{2}$+1×$\frac{1}{3}$+2×$\frac{1}{6}$=$\frac{2}{3}$,
Dξ=(0-$\frac{2}{3}$)2×$\frac{1}{2}$+(1-$\frac{2}{3}$)2×$\frac{1}{3}$+(2-$\frac{2}{3}$)2×$\frac{1}{6}$=$\frac{5}{9}$.
故答案为:$\frac{5}{9}$.
点评 本题主要考查离散型随机变量的分布和数学期望、方差等基础知识,熟记期望、方差的公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在($\frac{{\sqrt{x}}}{2}$-$\frac{2}{{\sqrt{x}}}$)4的二项展开式中,x的系数为( )
| A. | -$\frac{15}{4}$ | B. | -$\frac{3}{8}$ | C. | $\frac{15}{4}$ | D. | -1 |
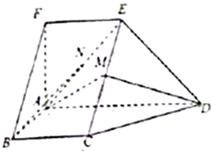 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.