题目内容
16.若函数f(x)=log${\;}_{\frac{1}{2}}$(2-ax)在[0,3]上的增函数,则a的取值范围是(0,$\frac{2}{3}$).分析 根据复合函数的单调性可知2-ax为减函数,故a>0,根据定义域和减函数得出2-3a>0,求解即可.
解答 解:函数f(x)=log${\;}_{\frac{1}{2}}$(2-ax)在[0,3]上的增函数,
∵$\frac{1}{2}$<1.对数函数为减函数,
∴2-ax为减函数,且2-ax>0,
∴2-3a>0,a>0,
∴0<a<$\frac{2}{3}$,
故答案为:(0,$\frac{2}{3}$).
点评 考查了复合函数的单调性和定义域问题,属于中档题,应熟练掌握.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
8.如图是-个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为( )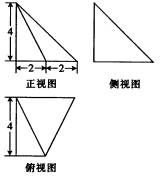

| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
1.已知角α、β的顶点与坐标原点重合,始边与x轴的非负半轴重合,点P(1,$\sqrt{3}$)、Q(3,-4)分别在角α、β的终边上,则sin(α-β)的值为( )
| A. | $\frac{3\sqrt{3}-4}{10}$ | B. | $\frac{3\sqrt{3}+4}{10}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
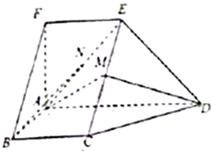 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.