题目内容
19.双曲线$\frac{x^2}{3}$-y2=1的两条渐近线的方程为$x±\sqrt{3}y=0$.分析 直接利用双曲线的渐近线的求法,求解即可.
解答 解:双曲线$\frac{x^2}{3}$-y2=1的两条渐近线的方程为:$x±\sqrt{3}y=0$.
故答案为:$x±\sqrt{3}y=0$.
点评 本题考查双曲线的简单性质的应用,渐近线的求法,是基础题.

练习册系列答案
相关题目
9.已知等差数列{an}的前n项和记为Sn,若a4+a6+a8=15,则S11的值为( )
| A. | 55 | B. | $\frac{55}{2}$ | C. | 165 | D. | $\frac{165}{2}$ |
10.将点P的直角坐标(-$\sqrt{3}$,-1)化成极坐标( )
| A. | (2,$\frac{π}{3}$) | B. | (2,$\frac{π}{2}$) | C. | (2,$\frac{4π}{3}$) | D. | (2,$\frac{7π}{6}$) |
14.已知如图所示的程序框图,当输入n=99时,输出S的值( )
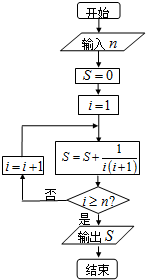

| A. | $\frac{100}{101}$ | B. | $\frac{99}{100}$ | C. | $\frac{98}{99}$ | D. | $\frac{97}{98}$ |
8.如图是-个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为( )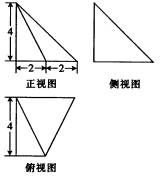

| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
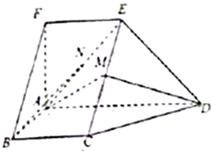 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,N为AE的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.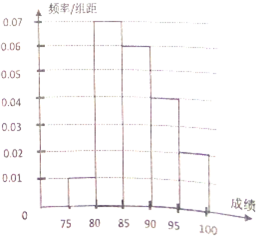 2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.
2016高考成绩已经揭晓,各大985名校展开争抢优秀生源的大战.某校在参加“华约”联盟笔试的学生中随机抽取100名学生,将他们的成绩由低到高分成1~5组得到如图的频率频率分布直方图.