题目内容
11.若实数x,y满足$\left\{\begin{array}{l}{x+y-2>0}\\{y-x-1<0}\\{x≤1}\end{array}\right.$,设u=x+2y,v=2x+y,则$\frac{u}{v}$的最大值为( )| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{7}{5}$ | D. | 2 |
分析 作出不等式组对应的平面区域,利用分式的性质转化为直线斜率,利用数形结合进行求解即可
解答 解:画出不等式组$\left\{\begin{array}{l}{x+y-2>0}\\{y-x-1<0}\\{x≤1}\end{array}\right.$,所表示的可行域,
如图所示,
则目标函数$\frac{u}{v}$=$\frac{x+2y}{2x+y}$=$\frac{1+2•\frac{y}{x}}{2+\frac{y}{x}}$,
令t=$\frac{y}{x}$,则t表示可行域内点P(x,y)与原点的斜率的取值,
当取可行域内点A($\frac{1}{2}$,$\frac{3}{2}$)时,t取得最大值,此时最大值为t=3;
当取可行域内点B(1,1)时,t取得最小值,此时最小值为t=1,
此时可得,
当t=3时,目标函数$\frac{u}{v}$有最大值,此时最大值为$\frac{1+2×3}{2+3}$=$\frac{7}{5}$;
故选C.
点评 本题主要考查线性规划的应用,根据分式的性质,转化为与斜率有关的问题是解决本题的关键.

练习册系列答案
相关题目
1.如图是棱长为1的正方体的平面展开图,则在这个正方体中,以下结论错误的是( )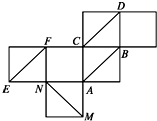

| A. | 点M到AB的距离为$\frac{{\sqrt{2}}}{2}$ | B. | AB与EF所成角是90° | ||
| C. | 三棱锥C-DNE的体积是$\frac{1}{6}$ | D. | EF与MC是异面直线 |
2.已知命题p:“x∈R时,都有x2-x+$\frac{1}{4}$<0”;命题q:“存在x∈R,使sinx+cosx=$\sqrt{2}$成立”.则下列判断正确的是( )
| A. | p∨q为假命题 | B. | p∧q为真命题 | C. | ¬p∧q为真命题 | D. | ¬p∨¬q是假命题 |
16.函数f(x)=x2-ax-1在区间(-$\frac{1}{2}$,$\frac{1}{2}$)上有零点,则实数a的取值范围是( )
| A. | ($\frac{3}{2}$,+∞) | B. | (-∞,-$\frac{3}{2}$) | C. | (-∞,-$\frac{3}{2}$)∪($\frac{3}{2}$,+∞) | D. | (-$\frac{3}{2}$,$\frac{3}{2}$) |
20.已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩(∁UB)等于( )
| A. | {2,5} | B. | {3,6} | C. | {2,5,6} | D. | {2,3,5,6,8} |
1.在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足,线段PD中点为M,当点P在圆上运动时,点M到直线l:x-y+1=0距离最大值为( )
| A. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{10}-\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
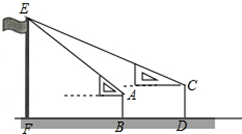 某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)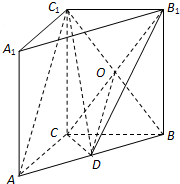 (理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.
(理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.