题目内容
19.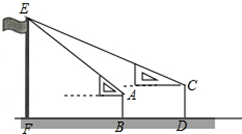 某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某校高一年级某班开展数学活动,小李和小军合作用一副三角板测量学校的旗杆,小李站在B点测得旗杆顶端E点的仰角为45°,小军站在点D测得旗杆顶端E点的仰角为30°,已知小李和小军相距(BD)6米,小李的身高(AB)1.5米,小军的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 过点A作AM⊥EF于M,过点C作CN⊥EF于N,设AM=ME=x(m),利用tan∠ECN=$\frac{EN}{CN}$.解得:x,然后求解旗杆的高EF.
解答 解:过点A作AM⊥EF于M,过点C作CN⊥EF于N,
∴MN=0.25m,
∵∠EAM=45°,∴AM=ME,
设AM=ME=x(m),则CN=(x+6)m,EN=(x-0.25)m,
∵∠ECN=30°,∴tan∠ECN=$\frac{EN}{CN}$=$\frac{x-0.25}{x+6}$=$\frac{\sqrt{3}}{3}$,
解得:x≈8.8,…..(5分)
则EF=EM+MF≈8.8+1.5=10.3(m).
答:旗杆的高EF为10.3m.…..(7分)
点评 本题考查三角形的实际应用,三角形的解法,考查计算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.命题“若c<0,则方程x2+x+c=0有实数解”,则( )
| A. | 该命题的逆命题为真,逆否命题也为真 | |
| B. | 该命题的逆命题为真,逆否命题也假 | |
| C. | 该命题的逆命题为假,逆否命题为真 | |
| D. | 该命题的逆命题为假,逆否命题也为假 |
7.f(x)为偶函数,当x>0时,f(x)=2x-1,则当x<0时,f(x)=( )
| A. | 2x-1 | B. | -2x+1 | C. | 2x+1 | D. | -2x-1 |
14.用“辗转相除法”求得360和504的最大公约数是( )
| A. | 36 | B. | 72 | C. | 24 | D. | 2 520 |
11.若实数x,y满足$\left\{\begin{array}{l}{x+y-2>0}\\{y-x-1<0}\\{x≤1}\end{array}\right.$,设u=x+2y,v=2x+y,则$\frac{u}{v}$的最大值为( )
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{7}{5}$ | D. | 2 |
8.设集合A={x|x∈N|x>1},则( )
| A. | ∅∉A | B. | 1∉A | C. | 1∈A | D. | {1}⊆A |