题目内容
1.在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足,线段PD中点为M,当点P在圆上运动时,点M到直线l:x-y+1=0距离最大值为( )| A. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{10}-\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 设出M点的坐标,由M为线段PD的中点得到P的坐标,把P的坐标代入圆x2+y2=4求得线段PD的中点M的轨迹方程;
再利用参数法求出点M到直线l:x-y+1=0距离最大值.
解答 解:设点M(x,y),由题意D(x,0),P(x,y1),
∵M为线段PD的中点,∴y1+0=2y,y1=2y;
又∵P(x,y1)在圆x2+y2=4上,∴x12+y12=4,
∴x2+4y2=4,即$\frac{{x}^{2}}{4}$+y2=1;
∴点M的轨迹为椭圆,
设x=2cosθ,y=sinθ,
则点M到直线l:x-y+1=0的距离为
d=$\frac{|2cosθ-sinθ+1|}{\sqrt{{1}^{2}{+(-1)}^{2}}}$=$\frac{|\sqrt{5}sin(θ+α)+1|}{\sqrt{2}}$≤$\frac{\sqrt{5}+1}{\sqrt{2}}$=$\frac{\sqrt{10}+\sqrt{2}}{2}$,其中tanα=-2;
所以d的最大值为$\frac{\sqrt{10}+\sqrt{2}}{2}$.
故选:A.
点评 本题考查了求点的轨迹方程以及点到直线距离的应用问题,是较难的题目.

练习册系列答案
相关题目
11.若实数x,y满足$\left\{\begin{array}{l}{x+y-2>0}\\{y-x-1<0}\\{x≤1}\end{array}\right.$,设u=x+2y,v=2x+y,则$\frac{u}{v}$的最大值为( )
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{7}{5}$ | D. | 2 |
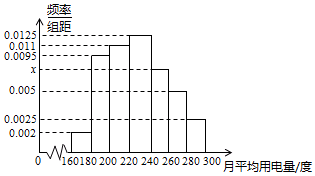 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.