题目内容
6.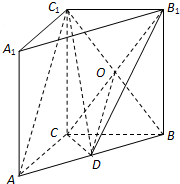 (理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.
(理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.求证:
(1)AC⊥BC1;
(2)AC1∥平面B1CD.
(3)若AC=BC=$\frac{1}{2}$CC1,求直线CC1与平面ABC1所成角的正切值.
分析 (1)由直三棱柱的性质可得CC1⊥平面ABC,即CC1⊥AC,又AC⊥BC,由线面垂直的判定可得AC⊥平面BCC1B1,则AC⊥BC1;
(2)设BC1与B1C的交点为O,连结OD,可得OD∥AC1,由线面平行的判定可得AC1∥平面B1CD;
(3)连结C1D,由CC1⊥平面ABC,得CC1⊥AB,再由CD⊥AB,得AB⊥平面C1CD,可知C1D是C1C在平面ABC1 上的射影,则∠CC1D为直线CC1与平面ABC1 所成的角.求解直角三角形得答案.
解答 (1)证明:在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,
∴CC1⊥AC,又AC⊥BC,BC∩CC1=C,
∴AC⊥平面BCC1B1,
∴AC⊥BC1;
(2)设BC1与B1C的交点为O,连结OD,
∵BCC1B1为平行四边形,∴O为B1C的中点,又D是AB的中点,
∴OD是三角形ABC1 的中位线,则OD∥AC1,
又∵AC1?平面B1CD,OD?平面B1CD,∴AC1∥平面B1CD;
(3)连结C1D,∵CC1⊥平面ABC,∴CC1⊥AB,
又∵AC=BC,D为AB的中点,
∴CD⊥AB,则AB⊥平面C1CD,
∴平面ABC1⊥平面C1CD,
∴C1D是C1C在平面ABC1 上的射影,则∠CC1D为直线CC1与平面ABC1 所成的角.
∵$CD=\frac{\sqrt{2}}{2}AC$,CC1=2AC,∴$tan∠C{C}_{1}D=\frac{CD}{C{C}_{1}}=\frac{\sqrt{2}}{4}$.
∴直线CC1与平面ABC1 所成的角的正切值为$\frac{\sqrt{2}}{4}$.
点评 本题考查空间中的直线与直线、直线与平面的位置关系,考查了线面角的求法,是中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
16.已知定义在R上的奇函数f(x)满足f(x)=f(x+2),当x∈(0,1]时,f(x)=$\sqrt{x},则f(\frac{7}{2})$等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
17.下列导数运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | B. | (xlnx)′=lnx+1 | C. | (cosx)′=sinx | D. | (2x)′=x2x-1 |
14.用“辗转相除法”求得360和504的最大公约数是( )
| A. | 36 | B. | 72 | C. | 24 | D. | 2 520 |
11.若实数x,y满足$\left\{\begin{array}{l}{x+y-2>0}\\{y-x-1<0}\\{x≤1}\end{array}\right.$,设u=x+2y,v=2x+y,则$\frac{u}{v}$的最大值为( )
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{7}{5}$ | D. | 2 |
18.已知非零向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a$⊥$\overrightarrow b$,|$\overrightarrow a$+$\overrightarrow b$|=3|$\overrightarrow b$|,则cos<$\overrightarrow a$,$\overrightarrow b$-$\overrightarrow a$>=( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |