题目内容
16.函数f(x)=x2-ax-1在区间(-$\frac{1}{2}$,$\frac{1}{2}$)上有零点,则实数a的取值范围是( )| A. | ($\frac{3}{2}$,+∞) | B. | (-∞,-$\frac{3}{2}$) | C. | (-∞,-$\frac{3}{2}$)∪($\frac{3}{2}$,+∞) | D. | (-$\frac{3}{2}$,$\frac{3}{2}$) |
分析 对函数类型及零点个数进行讨论,列不等式解出.
解答 解:函数f(x)=x2-ax-1的对称轴为x=$\frac{a}{2}$,
当$\frac{1}{2}$a<-$\frac{1}{2}$时,即a<-1,函数f(x)在区间(-$\frac{1}{2}$,$\frac{1}{2}$)上单调递增,
∴f(-$\frac{1}{2}$)<0,且f($\frac{1}{2}$)>0,
∴$\left\{\begin{array}{l}{\frac{1}{4}+\frac{1}{2}a-1<0}\\{\frac{1}{4}-\frac{1}{2}a-1>0}\end{array}\right.$,
解得a<-$\frac{3}{2}$,
当$\frac{1}{2}$a>$\frac{1}{2}$时,即a>1,函数f(x)在区间(-$\frac{1}{2}$,$\frac{1}{2}$)上单调递减,
∴f(-$\frac{1}{2}$)>0,且f($\frac{1}{2}$)<0,
∴$\left\{\begin{array}{l}{\frac{1}{4}+\frac{1}{2}a-1>0}\\{\frac{1}{4}-\frac{1}{2}a-1<0}\end{array}\right.$,
解得a>$\frac{3}{2}$,
当函数由两个零点时,$\left\{\begin{array}{l}{-1≤a≤1}\\{f(-\frac{1}{2})≥0}\\{f(\frac{1}{2})≥0}\end{array}\right.$,此时无解
综上所述a的取值范围为(-∞,-$\frac{3}{2}$)∪($\frac{3}{2}$,+∞)
故选:C
点评 本题考查二次函数的性质、函数的零点存在的条件,考查转化思想,属于中档题

| A. | $f(x)=x,g(x)={(\sqrt{x})^2}$ | B. | $f(x)=\left|x\right|,g(x)=\sqrt{[}3]{x^3}$ | ||
| C. | $f(x)={x^2},g(x)=\left\{\begin{array}{l}{x^2},(x>0)\\-{x^2},(x<0)\end{array}\right.$ | D. | $f(x)=\frac{{{x^2}-1}}{x-1},g(t)=t+1(t≠1)$ |
| A. | 2x-1 | B. | -2x+1 | C. | 2x+1 | D. | -2x-1 |
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{7}{5}$ | D. | 2 |
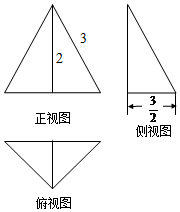
| A. | 12π | B. | $6\sqrt{3}π$ | C. | 9π | D. | 18π |
| A. | ∅∉A | B. | 1∉A | C. | 1∈A | D. | {1}⊆A |
| A. | {1,3,6,7,8} | B. | {1,3,7,8} | C. | {3,7,8} | D. | {0,1,2,6} |
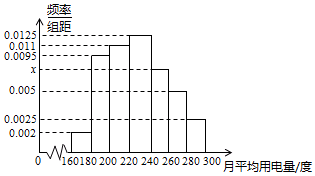 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.