题目内容
20.关于函数的对称性有如下结论:对于给定的函数y=f(x),x∈D,如果对于任意的x∈D都有f(a+x)+f(a-x)=2b成立(a,b为常数),则函数f(x)关于点(a,b)对称.(1)用题设中的结论证明:函数f(x)=$\frac{-2x+1}{x-3}$关于点(3,-2);
(2)若函数f(x)既关于点(2,0)对称,又关于点(-2,1)对称,且当x∈(2,6)时,f(x)=2x+3x,求:
①f(-5)的值;
②当x∈(8k-2,8k+2),k∈Z时,f(x)的表达式.
分析 (1)根据题设中的结论证明即可,
(2)由题意可得f(x+8)=f(x)-2,①代值计算即可,
②由f(x)=f(x-8)-2=f(x-8×2)-2×2=f(x-8×3)-2×3=…=f(x-8k)-2k,然后代值计算即可.
解答 解:(1)f(x)=$\frac{-2x+1}{x-3}$的定义域为{x|x≠3},对任意x≠3有f(3-x)+f(3-x)=(-2-$\frac{5}{x}$)+(-2-$\frac{5}{-x}$)=-4,
∴函数f(x)=$\frac{-2x+1}{x-3}$关于点(3,-2);
(2)函数f(x)关于点(2,0)对称,
∴f(2+x)+f(2-x)=0,
即f(x)+f(4-x)=0,
又关于点(-2,1)对称,
∴f(-2+x)+f(-2-x)=2,
即f(x)+f(-4-x)=2,
∴f(-4-x)=2+f(4-x),
即f(x+8)=f(x)-2,
①f(-5)=f(3)+2=23+3×3+2=19,
②x∈(8k-2,8k+2),x-8k∈(-2,2),4-(x-8k)∈(2,6),
∴f(x)=f(x-8)-2=f(x-8×2)-2×2=f(x-8×3)-2×3=…=f(x-8k)-2k,
又由f(t)=-f(4-t),
∴f(x)=f(x-8k)-2k=-f[4-(x-8k)]-2k=-[24-(x-8k)+3(4-(x-8k))]-2k,
∴即当x∈(8k-2,8k+2),k∈Z时,f(x)=-24-x+8k+3x-26k-12
点评 本题考查了抽象函数和新定义的应用,关键是掌握新定义的用法,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.若集合A={-2,-1,0,1,2},集合B={x|lg(x+1)>0},则A∩B等于( )
| A. | {-1,0,1,2} | B. | {-1,-2} | C. | {1,2} | D. | {0,1,2} |
8.若从区间(0,e)(e为自然对数的底数,e=2.71828…)内随机选取两个数,则这两个数之积小于e的概率为( )
| A. | $\frac{2}{e}$ | B. | $\frac{1}{e}$ | C. | 1-$\frac{2}{e}$ | D. | 1-$\frac{1}{e}$ |
5.若函数f(x)=(ax2+bx)ex的图象如图所示,则实数a,b的值可能为( )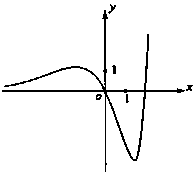

| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
9.一个多面体的三视图和直观图如图所示,M是AB的中点,一只蜻蜓在几何体ADF-BCE内自由飞翔,则它飞入几何体F-AMCD内的概率为( )

| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
