题目内容
8．若从区间（0，e）（e为自然对数的底数，e=2.71828…）内随机选取两个数，则这两个数之积小于e的概率为（ ）| A． | $\frac{2}{e}$ | B． | $\frac{1}{e}$ | C． | 1-$\frac{2}{e}$ | D． | 1-$\frac{1}{e}$ |
分析 由题意，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\end{array}\right.$，区域面积为e2，这两个数之积小于e，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\\{xy＜e}\end{array}\right.$，区域面积为e+${∫}_{1}^{e}\frac{e}{x}dx$=2e，即可得出结论．
解答 解：由题意，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\end{array}\right.$，区域面积为e2，
这两个数之积小于e，$\left\{\begin{array}{l}{0＜x＜e}\\{0＜y＜e}\\{xy＜e}\end{array}\right.$，区域面积为e+${∫}_{1}^{e}\frac{e}{x}dx$=2e，
∴这两个数之积小于e的概率为$\frac{2}{e}$，
故选A．
点评 本题主要考查几何概型的概率计算，根据条件求出对应的区域面积是解决本题的关键．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
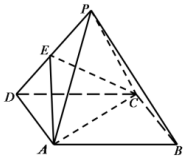如图，四棱锥P-ABCD中，底面ABCD是平行四边形，且平面PAC⊥平面ABCD，E为PD的中点，PA=PC，AB=2BC=2，∠ABC=60°．
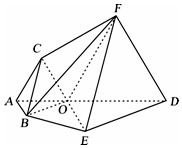如图，ABEDEFC为多面体，平面ABED⊥平面ACED，点O在线段AD上，OA=1，OD=2，△OAB，△OAC，△ODE，△ODF都是正三角形．