题目内容
15.已知P为抛物线y=2x2上的点,若点P到直线l:4x-y-6=0的距离最小,则点P的坐标为(1,2).分析 设抛物线y=2x2上一点为A(x0,2x02),求出点A(x0,2x02)到直线l:4x-y-6=0的距离,利用配方法,由此能求出抛物线y=2x2上一点到直线l:4x-y-6=0的距离最短的点的坐标.
解答 解:设抛物线y=2x2上一点为P(x0,2x02),
点A(x0,2x02)到直线l:4x-y-6=0的距离d=$\frac{丨4{x}_{0}-2{x}_{0}^{2}-6丨}{\sqrt{{4}^{2}+1}}$=$\frac{1}{\sqrt{17}}$|2(x0-1)2-8|,
∴当x0=1时,即当A(1,2)时,抛物线y=2x2上一点到直线l:4x-y-6=0的距离最短.
故答案为:(1,2).
点评 本题考查抛物线上的点到直线的距离最短的点的坐标的求法,考查学生的计算能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设函数f′(x)是定义(0,2π)在上的函数f(x)的导函数,f(x)=f(2π-x),当0<x<π时,若f(x)sinx-f′(x)cosx<0,a=$\frac{1}{2}$f($\frac{π}{3}$),b=0,c=-$\frac{{\sqrt{3}}}{2}$f($\frac{7π}{6}$),则( )
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | c<a<b |
6.某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位:cm)频数分布表如表1、表2.
表1:男生身高频数分布表
表2:女生身高频数分布表
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.
10.从{2,3,4,5,6}中随机选取一个数为a,从{1,2,3,5}中随机选取一个数为b,则b>a的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
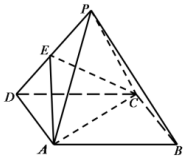 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.