题目内容
设椭圆e:
+
=1(a>b>0),其长轴是短轴长的
倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2
.求椭圆e的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知a=
b,
=2
,解得a,b,可得椭圆e的方程;
| 2 |
| 2b2 |
| a |
| 3 |
解答:
解:由已知a=
b,
=2
,解得a=2
,b=
,
∴椭圆的方程为
+
=1.
| 2 |
| 2b2 |
| a |
| 3 |
| 3 |
| 6 |
∴椭圆的方程为
| x2 |
| 12 |
| y2 |
| 6 |
点评:本题考查椭圆方程,椭圆的基本性质的考查.

练习册系列答案
相关题目
已知a<0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A、?x∈R,f(x)≤f(x0) |
| B、?x∈R,f(x)≥f(x0) |
| C、?x∈R,f(x)≤f(x0) |
| D、?x∈R,f(x)≥f(x0) |
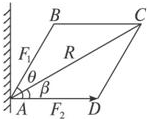 如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β.
如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β.