题目内容
20.若命题p:“关于x的不等式ax2+ax+1≤0的解集为R”为假命题,则实数a的取值范围为R.分析 先求出命题p是真命题时a的取值范围,再求命题p为假命题时a的取值范围即可R.
解答 解:当命题p:“关于x的不等式ax2+ax+1≤0的解集为R”是真命题时,
应满足$\left\{\begin{array}{l}{a<0}\\{△≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a<0}\\{{a}^{2}-4a≤0}\end{array}\right.$
该不等式的解集是∅;
所以命题p:“关于x的不等式ax2+ax+1≤0的解集为R”为假命题时,实数a的取值范围为R.
故答案为:R.
点评 本题考查了一元二次不等式的恒成立问题,也考查了简易逻辑的应用问题,是基础题目.

练习册系列答案
相关题目
11.函数y=$\frac{{x}^{2}-1}{\sqrt{2-|x|}}$的定义域是( )
| A. | [-2,2] | B. | (-∞,-2]∪[2,+∞) | C. | (-2,2) | D. | (-∞,-2)∪(2,+∞) |
8.若tanα=3,则tan(α-$\frac{π}{4}$)=( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
15.曲线(x+2y+a)(x2-y2)=0为平面上交于一点的三条直线的充要条件是( )
| A. | a=0 | B. | a=1 | C. | a=-1 | D. | a∈R |
5.如图是一个程序框图,则输出的S的值是( )


| A. | -1 | B. | 0 | C. | 8 | D. | 9 |
12.设集合A={a,a2,-2},B={2,4},A∩B={4},则a=( )
| A. | 2 | B. | -2 | C. | 4 | D. | $\sqrt{2}$ |
9.设等差数列{an}的前n项和为Sn,且满足S2016>0,S2017<0,对任意正整数n,都有|an|≥|ak|,则k的值为( )
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
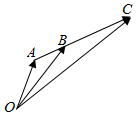 已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)
已知A(2,3),B(5,4),连接AB并延长至C,使得AC=3AB,求C点的坐标.(提示:如图所示,$\overrightarrow{OC}$=$\overrightarrow{OA}$+3$\overrightarrow{AB}$)