题目内容
函数f(x)=(1+x-
+
)cos2x在区间[-3,3]上的零点的个数为 .
| x2 |
| 2 |
| x3 |
| 3 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:把函数分解为g(x)=1+x-
+
,h(x)=cos2x,利用导数,三角函数判断即可.
| x2 |
| 2 |
| x3 |
| 3 |
解答:
解:∵函数f(x)=(1+x-
+
)cos2x,
∴设g(x)=1+x-
+
,h(x)=cos2x,
∴g′(x)=1-x+x2>0恒成立,
即g(x)为单调递增函数,
g(0)=1,g(-1)=1-1-
-
<0
有一个零点在(-1,0)
由cos2x=0求x的个数,由2x=kπ+
得x=
+
,k∈z,又x∈[-3,3],∴
,
,-
,-
为零点
所以cos2x=0有4个零点,
g(-
)≠0,
可以判断函数f(x)=(1+x-
+
)cos2x在区间[-3,3]上的零点的个数为5个
故答案为:5
| x2 |
| 2 |
| x3 |
| 3 |
∴设g(x)=1+x-
| x2 |
| 2 |
| x3 |
| 3 |
∴g′(x)=1-x+x2>0恒成立,
即g(x)为单调递增函数,
g(0)=1,g(-1)=1-1-
| 1 |
| 2 |
| 1 |
| 3 |
有一个零点在(-1,0)
由cos2x=0求x的个数,由2x=kπ+
| π |
| 2 |
| kπ |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
所以cos2x=0有4个零点,
g(-
| π |
| 4 |
可以判断函数f(x)=(1+x-
| x2 |
| 2 |
| x3 |
| 3 |
故答案为:5
点评:本题主要考查函数的零点,分类讨论的数学思想,分解为简单的函数,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 如图,△ADP为正三角形,O为正方形ABCD中心,而ADP⊥面ABCD,M为面ABCD内的点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( )
如图,△ADP为正三角形,O为正方形ABCD中心,而ADP⊥面ABCD,M为面ABCD内的点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( )


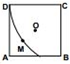
 如图平行四边形ABCD中,∠DAB=60°,AB=2AD=2,M为边CD的中点,沿BM将△CBM折起使得平面BMC⊥平面ABMD.
如图平行四边形ABCD中,∠DAB=60°,AB=2AD=2,M为边CD的中点,沿BM将△CBM折起使得平面BMC⊥平面ABMD.