题目内容
函数y=x2-4x+6，x∈[1，5]的值域是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：求出二次函数的对称轴，研究函数在x∈[1，5]的单调性，解出最值，写出值域即可．
解答：
解：函数y=x2-4x+6的对称轴是x=2，由二次函数的性质知，函数在[1，2]上是减函数，在[2，5]上函数是增函数
又x=2，y=2，
x=1，y=3，
x=5，y=11，
故函数的值域是[2，11]，
故答案为：[2，11]
又x=2，y=2，
x=1，y=3，
x=5，y=11，
故函数的值域是[2，11]，
故答案为：[2，11]
点评：本题考查二次函数在闭区间上的最值，解答本题关键是根据二次函数的性质判断出函数在何处取到最值，二次函数在闭区间上最值在高中数学中应用十分广泛，一些求最值的问题最后往往归结到二次函数的最值上来．
练习册系列答案
相关题目
已知x，y满足
，则2x-y的最大值为（ ）
|
| A、1 | B、2 | C、3 | D、4 |
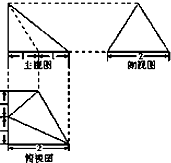
一个四棱锥的三视图如图所示，其侧视图是等边三角形，该四棱锥的体积等于（ ）
A、
| ||
B、2
| ||
C、3
| ||
D、6
|
已知函数y=6sin（ωx+ϕ）（ω＞0）的部分图象如图所示，设P是图象的最高点，A，B是图象与x轴的交点，若tan∠APB=2，则ω=