题目内容
9.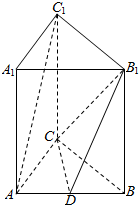 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.(1)求证:AC⊥B1C;
(2)求证:AC1∥平面CDB1.
分析 (1)由已知可证AC⊥CC1,利用勾股定理可证AC⊥BC,可证AC⊥平面BCC1,又B1C?平面BCC1,即可证明AC⊥B1C;
(2)连接BC1,交CB1于E,连接DE,运用中位线定理,以及线面平行的判定定理,即可得证;
解答 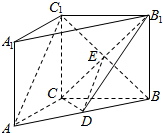 证明:(1)∵三棱柱ABC-A1B1C1的侧棱与底面垂直,AC?平面ABC,
证明:(1)∵三棱柱ABC-A1B1C1的侧棱与底面垂直,AC?平面ABC,
∴AC⊥CC1,
∵AC=9,BC=12,AB=15,可得:AC2+BC2=AB2,
∴AC⊥BC,
∵CC1∩BC=C,
∴AC⊥平面BCC1,
∵B1C?平面BCC1,
∴AC⊥B1C;
(2)连接BC1,交CB1于E,连接DE,
由于D为中点,E为中点,
则DE∥AC1,DE?平面CDB1,AC1?平面CDB1,
则有AC1∥平面CDB1;
点评 本题考查直线与平面平行的判定定理,考查直线与平面垂直的判定定理,考查空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
17.抛物线x2=2py(p>0)的焦点F,其准线与双曲线$\frac{x^2}{3}-\frac{y^2}{3}=1$相交于A,B两点,若△ABC是等边三角形,则p等于( )
| A. | 6 | B. | 8 | C. | 4 | D. | 2 |
4.三个函数:y=cosx,y=sinx,y=tanx,从中随机抽取一个函数,则抽出的函数是奇函数的概率为( )
| A. | $\frac{1}{3}$ | B. | 0 | C. | $\frac{2}{3}$ | D. | 1 |
14.已知函数f(x)为定义在R上的奇函数,且当x>0时,f(x)=x2-2x+3,则f(-1)=( )
| A. | 2 | B. | 6 | C. | -2 | D. | -6 |
18.下列说法正确的是( )
| A. | 向量$\overrightarrow{AB}$∥$\overrightarrow{CD}$就是$\overrightarrow{AB}$所在的直线平行于$\overrightarrow{CD}$所在的直线 | |
| B. | 共线向量是在一条直线上的向量 | |
| C. | 长度相等的向量叫做相等向量 | |
| D. | 零向量长度等于0 |