题目内容

14．已知函数f（x）为定义在R上的奇函数，且当x＞0时，f（x）=x2-2x+3，则f（-1）=（　　）
A．2B．6C．-2D．-6

分析 利用函数的奇偶性直接求解函数值即可．

解答 解：函数f（x）为定义在R上的奇函数，且当x＞0时，f（x）=x2-2x+3，
则f（-1）=-f（1）=-[12-2×1+3]=-2．
故选：C．

点评 本题考查函数的奇偶性的应用，是基础题．

练习册系列答案
相关题目
4．在三棱锥P-ABC中，BC=3，CA=4，AB=5，若三个侧面与底面ABC所成二面角均为60°，则三棱锥的体积是2$\sqrt{3}$．
5．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=ax-1，其中a＞0且a≠1
（1）求f（2）+f（-2）的值；
（2）求x＜0时f（x）的解析式．
2．直线x+y-2=0与圆x2+y2-4y=0的位置关系是（　　）
A．相交且过圆心B．相离C．相切D．相交且不过圆心
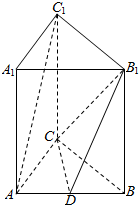9．如图，三棱柱ABC-A1B1C1的侧棱与底面垂直，AC=9，BC=12，AB=15，点D是AB的中点．
（1）求证：AC⊥B1C；
（2）求证：AC1∥平面CDB1．
19．已知直线4x+3y-35=0与圆心在原点的圆C相切，则圆C的方程为x2+y2=49．
6．三条两两相交的直线最多可确定（　　）个平面．
A．1B．2C．3D．无数
3．设函数f（x）=cos$\frac{π}{3}$x，则f（1）+f（2）+f（3）+…+f（2 015）+f（2 016）=0．
4．四面体ABCD的四个顶点都在球O的球面上，AB⊥平面BCD，△BCD是边长为3的等边三角形，若AB=2，则球O的表面积为16π．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网