题目内容
1.已知直线l:3x-y-6=0与圆C:x2+y2-2x-4y=0.求:(1)截得的弦AB的长;
(2)△AOB面积(O为坐标原点).
分析 (1)由直线与圆相交的性质可知,($\frac{AB}{2}$)2=r2-d2,要求AB,只要求解圆心到直线3x-y-6=0的距离d即可.
(2)求出O到直线3x-y-6=0的距离,即可求出△AOB面积.
解答 解:(1)由题意圆x2+y2-2x-4y=0可得,圆心(1,2),半径r=$\sqrt{5}$,圆心到直线3x-y-6=0的距离d=$\frac{|3×1-2-6|}{\sqrt{9+1}}$=$\frac{\sqrt{10}}{2}$,
则由圆的性质可得,($\frac{AB}{2}$)2=r2-d2=$\frac{5}{2}$,
即AB=$\sqrt{10}$.
(2)O到直线3x-y-6=0的距离为$\frac{6}{\sqrt{10}}$,
∴△AOB面积为S=$\frac{1}{2}×\sqrt{10}×\frac{6}{\sqrt{10}}$=3.
点评 本题主要考查了直线与圆相交性质的应用,点到直线的距离公式的应用,属于中档题.

练习册系列答案
相关题目
11.设$f(x)=\left\{\begin{array}{l}x+1,(x>0)\\ 1-x,(x=0)\\-1,(x<0)\end{array}\right.$,则f[f(0)]=( )
| A. | 1 | B. | 0 | C. | 2 | D. | -1 |
12.函数f(x)=ex-2x+1在[0,1)上的最小值是( )
| A. | 2 | B. | e-1 | C. | 3-2ln2 | D. | 2-2ln2 |
16.下列函数中,在(0,+∞)为增函数的是( )
| A. | y=x2-3x+1 | B. | y=-2x+9 | C. | $y={(\frac{1}{2})^x}$ | D. | y=log2x |
6.三条两两相交的直线最多可确定( )个平面.
| A. | 1 | B. | 2 | C. | 3 | D. | 无数 |
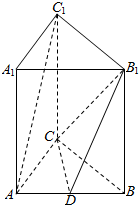 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.