题目内容
19.已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+f(1),若直线y=kx与函数y=f(x)的图象恰有11个不同的公共点,则实数k的取值范围为($2\sqrt{6}-4$,$4\sqrt{3}-6$).分析 作出f(x)的图象,根据交点个数判断直线的临界位置.根据导数与切线的关系列出方程解出.
解答  解:当2≤x≤3时,f(x)=(x-2)2+2,当3≤x≤4时,f(x)=(x-3)2+3,作出f(x)在[0,4]上的函数图象如图,
解:当2≤x≤3时,f(x)=(x-2)2+2,当3≤x≤4时,f(x)=(x-3)2+3,作出f(x)在[0,4]上的函数图象如图,
设y=k1x与f(x)在[2,3]上的图象相切于(x1,y1),y=k2x与f(x)在[3,4]上的图象相切于(x2,y2),
则$\left\{\begin{array}{l}{2{x}_{1}-4={k}_{1}}\\{{(x}_{1}-2)^{2}+2={y}_{1}}\\{{k}_{1}{x}_{1}={y}_{1}}\end{array}\right.$,$\left\{\begin{array}{l}{2{x}_{2}-6={k}_{2}}\\{({x}_{2}-3)^{2}+3={y}_{2}}\\{{k}_{2}{x}_{2}={y}_{2}}\end{array}\right.$,解得k1=2$\sqrt{6}$-4,k2=4$\sqrt{3}$-6.
由函数的对称性可知,若直线y=kx与函数y=f(x)的图象恰有11个不同的公共点,
则k1<k<k2.
故答案为($2\sqrt{6}-4$,$4\sqrt{3}-6$).
点评 本题考查了函数的图象变换,导数与切线的关系,图象的交点个数与零点的关系,属于中档题.作出函数图象是关键.

练习册系列答案
相关题目
9.在复平面上,满足|z-1|=|z+i|(i为虚数单位)的复数z对应的点的轨迹为( )
| A. | 椭圆 | B. | 圆 | C. | 线段 | D. | 直线 |
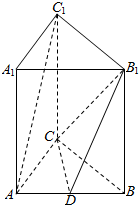 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,点D是AB的中点.